EWPS-04: 2D Waveguides – P/S Waves, Rayleigh Waves, and Lamb Waves
In Parts 2 and 3, we analyzed rods and beams—one-dimensional structures where waves travel along a single axis. Real-world applications, however, often involve 2D waveguides: thick plates, layered composites, and the earth’s crust itself.
This post explores wave propagation in isotropic 2D media. We’ll untangle the coupled differential equations governing these systems, discover why earthquakes produce distinct “primary” and “secondary” shocks, and examine the surface waves that travel along free boundaries.
The Challenge of Coupling: Navier’s Equation
In a 2D solid, deformations occur in both the $x$ (horizontal) and $z$ (vertical/depth) directions. Unlike a rod where axial and lateral motions are independent, in 2D these motions become intimately coupled.
Physical intuition: Press down on a block of jelly—it spreads sideways. This is coupling: vertical compression produces horizontal expansion. In wave propagation, this means a disturbance in one direction immediately affects motion in other directions.
The behavior of 2D isotropic elastic solids is governed by Navier’s equation:
$$ (\lambda + \mu)\nabla(\nabla \cdot \mathbf{u}) + \mu \nabla^2 \mathbf{u} = \rho \ddot{\mathbf{u}} $$
where:
- $\mathbf{u} = (u, w)$ is the displacement vector
- $\lambda, \mu$ are Lamé’s constants, related to Young’s modulus $E$ and Poisson’s ratio $\nu$ by:
$$ \lambda = \frac{E\nu}{(1+\nu)(1-2\nu)}, \quad \mu = \frac{E}{2(1+\nu)} $$
- $\rho$ is the material density
Understanding the two terms:
- $(\lambda + \mu)\nabla(\nabla \cdot \mathbf{u})$ — volumetric (dilatational) effects: compression/expansion
- $\mu \nabla^2 \mathbf{u}$ — shear (distortional) effects: shape change without volume change
These terms are coupled—solving them directly requires simultaneous equations in $u$ and $w$.
The Solution: Helmholtz Decomposition
The key to solving Navier’s equation is Helmholtz decomposition, which splits the displacement field into two independent potentials:
$$ \mathbf{u} = \nabla\Phi + \nabla \times \mathbf{H} $$
Why this works: The Helmholtz theorem guarantees that any vector field can be decomposed into an irrotational part (gradient of a scalar) and a solenoidal part (curl of a vector). This isn’t an approximation—it’s mathematically exact.
In 2D component form:
$$ u = \frac{\partial \Phi}{\partial x} + \frac{\partial H_y}{\partial z}, \quad w = \frac{\partial \Phi}{\partial z} - \frac{\partial H_y}{\partial x} $$
where:
- Scalar potential $\Phi$: Pure volume change (dilatation) without rotation — generates P-waves
- Vector potential $H_y$: Pure rotation (distortion) without volume change — generates S-waves
Interpreting the figure: The left side shows the original coupled problem (Navier’s equation with $u$ and $w$ intertwined). Helmholtz decomposition acts as a “disentangling” step, producing two separate boxes on the right—each governed by a simple wave equation that we already know how to solve.
The Magic: Uncoupled Wave Equations
Substituting the Helmholtz decomposition into Navier’s equation yields two independent wave equations:
| Potential | Governs | Wave Equation | Wave Speed |
|---|---|---|---|
| $\Phi$ (scalar) | P-waves | $\nabla^2 \Phi = \displaystyle\frac{1}{C_p^2}\ddot{\Phi}$ | $C_p = \sqrt{\displaystyle\frac{\lambda + 2\mu}{\rho}}$ |
| $H_y$ (vector) | S-waves | $\nabla^2 H_y = \displaystyle\frac{1}{C_s^2}\ddot{H_y}$ | $C_s = \sqrt{\displaystyle\frac{\mu}{\rho}}$ |
Why does this decouple? The key identities are $\nabla \cdot (\nabla \times \mathbf{H}) = 0$ (curl is divergence-free) and $\nabla \times (\nabla \Phi) = 0$ (gradient is curl-free). When substituted into Navier’s equation, the volumetric term only “sees” $\Phi$, and the shear term only “sees” $H_y$—they separate naturally.
P-Waves and S-Waves: The Body Waves
The mathematical decoupling found above corresponds to two distinct physical modes of propagation:

P-Waves (Primary/Pressure Waves)
Governed by the scalar potential $\Phi$, P-waves involve particle motion parallel to the direction of propagation (longitudinal). This creates alternating compressed and extended zones without rotating the medium.
- Analogy: A Slinky spring being pushed and pulled along its length.
- Physical Mechanism: Resistance to volume change (compression) and shear.
- Medium: Can propagate in solids, liquids, and gases (sound waves are P-waves).
- Speed: $C_p = \sqrt{(\lambda + 2\mu)/\rho}$. Being the fastest wave, it creates the initial “thump” in an earthquake.
S-Waves (Secondary/Shear Waves)
Governed by the vector potential $\mathbf{H}$, S-waves involve particle motion perpendicular to the direction of propagation (transverse). This creates shape distortion (shear) without changing the material’s volume.
- Analogy: A rope or whip being flicked sideways or up and down.
- Physical Mechanism: Resistance to shear deformation (shape change).
- Medium: Can propagate only in solids. Fluids and gases generally cannot support shear stresses ($\mu \approx 0$).
- Speed: $C_s = \sqrt{\mu/\rho}$. They arrive second but typically carry more energy and cause stronger shaking.
The Speed Relationship
For typical isotropic materials, the speed ratio $C_p/C_s$ is determined solely by Poisson’s ratio ($\nu$):
$$ \frac{C_p}{C_s} = \sqrt{\frac{\lambda + 2\mu}{\mu}} = \sqrt{\frac{2(1-\nu)}{1-2\nu}} $$
For a typical rock with $\nu \approx 0.25$, the P-wave is about 73% faster than the S-wave ($C_p \approx 1.73 C_s$).
Physical Intuition: Why are P-waves faster?
P-waves travel by compressing the material. To do this, they must overcome the material’s resistance to both compression and shear (represented by $\lambda + 2\mu$). S-waves only shear the material, fighting only the resistance to shear ($\mu$). Since materials are generally stiffer in compression than in shear, P-waves travel faster.
Semi-Infinite Media: The Rayleigh Wave
When body waves encounter a free surface (like the ground interacting with air), the boundary conditions require stress to be zero. This constraint forces P and S waves to interact, generating a new mode: the Rayleigh wave.
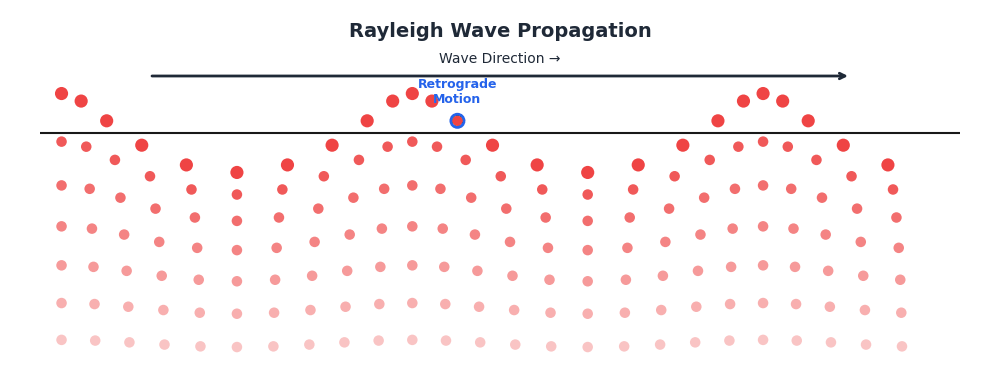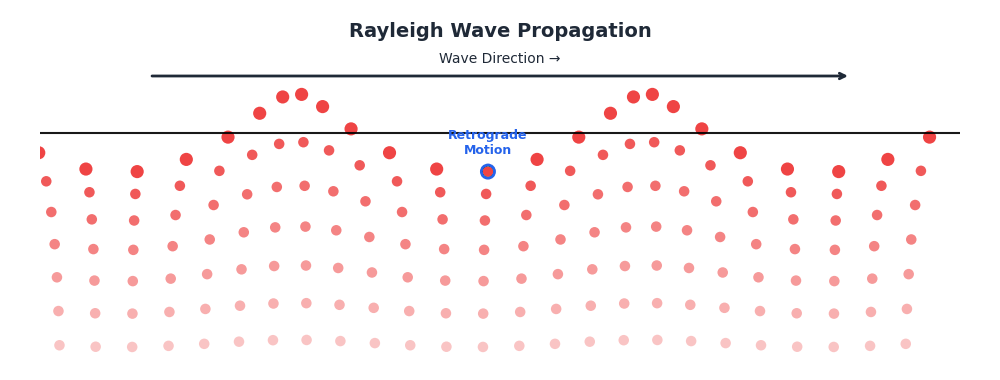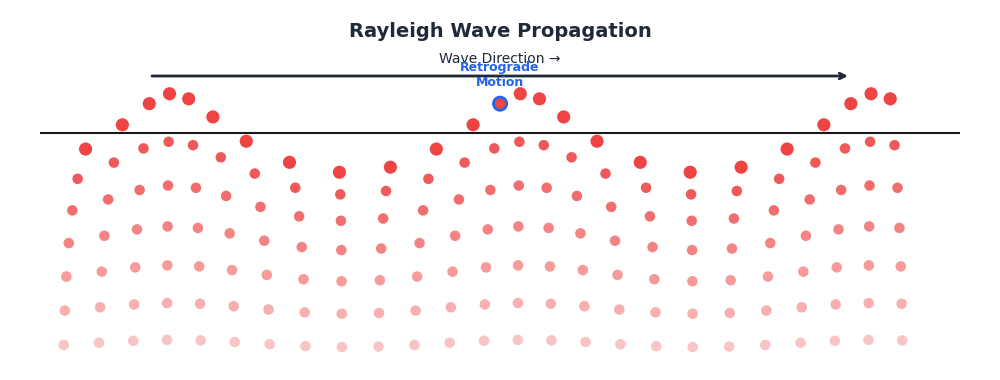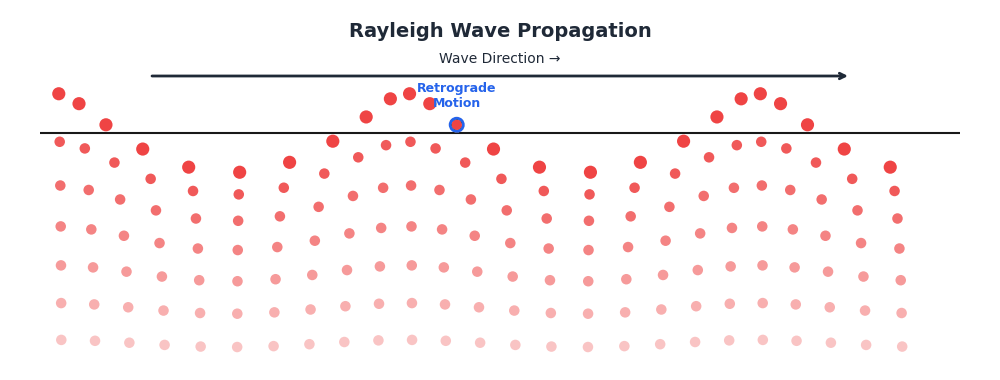
Distinctive Particle Motion
Unlike body waves, Rayleigh wave particles move in a retrograde elliptical path:
- Motion is “backward-rolling” at the surface (opposite to propagation).
- Analogy: Similar to ocean waves, but ocean waves are prograde (forward-rolling).
- Depth profile: The motion amplitude decays exponentially with depth, essentially confining the energy to a surface layer about one wavelength thick.
Why They Dominate Damage (Geometrical Spreading)
Body waves propagate spherically through the volume, while Rayleigh waves expand cylindrically along the surface. This difference in geometry leads to different decay rates:
- Body Waves (3D Spreading): Energy spreads over a sphere surface area ($4\pi r^2$). Amplitude decays as $\propto 1/r$.
- Rayleigh Waves (2D Spreading): Energy spreads over a cylinder perimeter ($2\pi r$). Amplitude decays as $\propto 1/\sqrt{r}$.
Consequence: At large distances from an epicenter, Rayleigh waves retain much more energy than P or S waves, causing the strongest shaking and most structural damage.
The Rayleigh Equation
The speed $C_R$ is determined by finding the root of the characteristic equation (where boundary stresses vanish):
$$ \left( 2 - \frac{C_R^2}{C_s^2} \right)^2 - 4\sqrt{1 - \frac{C_R^2}{C_p^2}}\sqrt{1 - \frac{C_R^2}{C_s^2}} = 0 $$
While complex-looking, it implies a simple result for typical Poisson’s ratios: the Rayleigh wave travels slightly slower than the shear wave, typically $C_R \approx 0.92 C_s$.
Doubly Bounded Media: Lamb Waves
When we have two parallel free surfaces (like a plate with top and bottom boundaries), waves bounce back and forth between them. The plate acts as a waveguide, trapping the energy and creating guided waves called Lamb waves.
Two Fundamental Mode Families
Lamb waves are split into two independent families based on particle motion symmetry relative to the mid-plane:
| Mode | Analogy | Description |
|---|---|---|
| Symmetric (S₀, S₁, …) | “Breathing” | The plate expands and contracts symmetrically. Similar to a lung breathing or a pulse moving through an artery. |
| Antisymmetric (A₀, A₁, …) | “Bending” | The plate bends as a whole. Similar to a flag waving or shaking a rug. |
Key Features: Why They Are Complex
- Dispersive: Speed depends on frequency. A sharp pulse will spread out (“disperse”) as it travels because high and low frequency components arrive at different times.
- Multi-modal: At higher frequencies, multiple modes (S₁, A₁, …) can exist simultaneously, making signal interpretation difficult.
- Frequency Equation: Determining the speed requires solving a transcendental equation that relates thickness ($2h$) and frequency ($\omega$):
$$ \dfrac{\tan(qh)}{\tan(ph)} = \begin{cases} -\dfrac{4k^2 pq}{(q^2 - k^2)^2} & \text{for Symmetric modes} \\ -\dfrac{(q^2 - k^2)^2}{4k^2 pq} & \text{for Antisymmetric modes} \end{cases} $$
(where $p$ and $q$ relate to the standing wave patterns across the plate thickness)
Application: Structural Health Monitoring (SHM)
Despite their complexity, Lamb waves are the “gold standard” for detecting damage in thin structures (like aircraft skins or pipelines) because:
- Long Range: They can travel meters without much amplitude loss.
- Sensitivity: They interact strongly with cracks, corrosion, and delamination.
- A₀ Mode: Particularly sensitive to surface cracks and widely used for inspection.
Summary & Key Takeaways
We have traversed from infinite bodies to bounded plates, seeing how boundaries reshape wave propagation:
| Wave Type | Particle Motion | Domain | Key Characteristic | Application |
|---|---|---|---|---|
| P-wave | Longitudinal (Push-Pull) | Infinite Body | Fastest ($C_p$) | Earthquake Warning |
| S-wave | Transverse (Shear) | Infinite Body | High Energy | Seismic Shaking |
| Rayleigh | Retrograde Elliptical | Half-Space (Surface) | Surface Confined | Earthquake Damage |
| Lamb | Symmetric / Antisymmetric | Plate (Waveguide) | Dispersive | Structural Inspection (SHM) |
Final Insights
- Boundaries Create Complexity: A simple free surface turns P/S waves into Rayleigh waves; two surfaces turn them into Lamb waves. The geometry dictates the physics.
- Geometric Spreading Matters: Surface waves (Rayleigh) decay slower than body waves ($1/\sqrt{r}$ vs $1/r$), explaining why distant earthquakes are still destructive.
- Dispersion is Key: In waveguides (Lamb waves), speed depends on frequency. This complicates signal analysis but encodes rich information about the medium’s thickness and health.
What’s Next?
Our journey so far has assumed materials are isotropic—meaning properties are the same in all directions. But real-world high-performance materials (like Carbon Fiber Reinforced Polymers) are not so simple.
In Part 5, we venture into the complex world of Anisotropy and Laminated Composites. We will explore:
- What happens when material stiffness depends on direction?
- Why the beautiful Helmholtz decomposition fails in anisotropic media.
- How we develop new mathematical tools to predict wave propagation in modern aerospace structures.
References
Gopalakrishnan, S. (2023). Elastic Wave Propagation in Structures and Materials. CRC Press.