In our previous post, we explored the elegant physics of the Micro-Perforated Panel (MPP), where we learned to absorb sound by turning it into heat through friction in tiny holes. Absorption is excellent for reducing echoes inside a room, making speech clearer and music richer.

But sometimes, we don’t just want to “tame” the sound inside a room; we want to keep it out entirely. We want to stop the roar of traffic from entering our bedroom or keep the thumping bass of a cinema from leaking into the library next door. This brings us to the domain of Sound Insulation.

Today we explore the brute force of the Mass Law and the clever engineering of Double Walls.

The Single Wall: It’s All About Mass

How does a wall block sound? You might think the wall simply “stops” the air. But remember, sound is a wave of pressure. When a sound wave hits a wall, it pushes against it. For the sound to transmit to the other side, the wall itself must vibrate, acting like a giant diaphragm that re-radiates the sound on the other side.

Therefore, to stop the sound, we must stop the wall from moving. According to Newton’s Second Law ($F=ma$), to minimize acceleration ($a$) for a given force ($F$), you need a large mass ($m$).

The Mass Law

This physical reality is codified in the Mass Law. For a single-layer homogeneous wall, the sound insulation (Transmission Loss, $TL$) is primarily determined by the surface density ($m$, mass per unit area) and the frequency ($f$):

$$ TL \approx 20 \log_{10}(m \cdot f) - 42 \quad [\text{dB}] $$

The rule of thumb derived from the Mass Law is simple but powerful:

• The 6 dB Rule: If you double the mass of the wall (e.g., using a brick twice as thick), the sound insulation increases by 6 dB.
• Alternatively, if you double the frequency of the sound (go one octave higher), the insulation also increases by 6 dB.

This explains why heavy materials like concrete and lead are excellent sound barriers, and why low-frequency rumble is harder to block than high-pitched sounds—bass notes simply push harder against the heavy wall.

The Achilles’ Heel: Coincidence Effect

However, a single wall is not a perfect barrier. At a specific frequency (the critical frequency, $f_c$), the wavelength of the sound in air matches the wavelength of the flexural waves traveling through the wall itself:

$$ f_c = \frac{c^2}{1.8 \cdot t} \sqrt{\frac{\rho_s}{E}} $$

where $t$ is wall thickness, $\rho_s$ is material density, and $E$ is Young’s modulus.

When this happens, the wall becomes “transparent” to sound. It vibrates sympathetically with the incoming wave, and the insulation capability drops sharply, creating a “dip” in the insulation curve. For a heavy wall like concrete, this frequency is usually very low, but for light partitions like glass or gypsum board, it can fall right in the middle of the speech range (1–4 kHz), compromising privacy.

The Double Wall: The Mass-Spring-Mass System

If we strictly followed the Mass Law, building a soundproof room would require walls several meters thick. That is structurally impossible for airplanes, ships, or even most office buildings.

The engineering solution is the Double Wall. Instead of one heavy wall, we use two lighter walls separated by an air gap.

The Physics of Separation

This structure acts as a Mass-Spring-Mass system:

• Mass 1: The first wall.
• Spring: The air trapped in the gap (which is compressible).
• Mass 2: The second wall.

The Resonance Trap

This system has a natural resonance frequency ($f_0$).

• Below $f_0$: The two walls are coupled by the stiff air spring and move together. The insulation is no better (and sometimes worse) than a single wall of the combined weight.
• Above $f_0$: The magic happens. The air spring becomes “soft” at high frequencies, decoupling the two masses. The sound energy is lost trying to compress the air and push the second independent mass.

While a single wall gains 6 dB per octave, a well-designed double wall can theoretically gain 18 dB per octave above the resonance frequency:

$$ f_0 = \frac{c}{2\pi}\sqrt{\frac{\rho}{d}\left(\frac{1}{m_1} + \frac{1}{m_2}\right)} $$

where $d$ is the air gap width, and $m_1$, $m_2$ are the surface densities of the two walls. This allows double-pane windows and drywall partitions to block noise far more effectively than their light weight would suggest.

The animation below (simulated using k-Wave) shows a pressure pulse propagating through a double wall. Watch how the wave reflects multiple times at each wall, and how significantly attenuated the transmitted wave is on the other side:

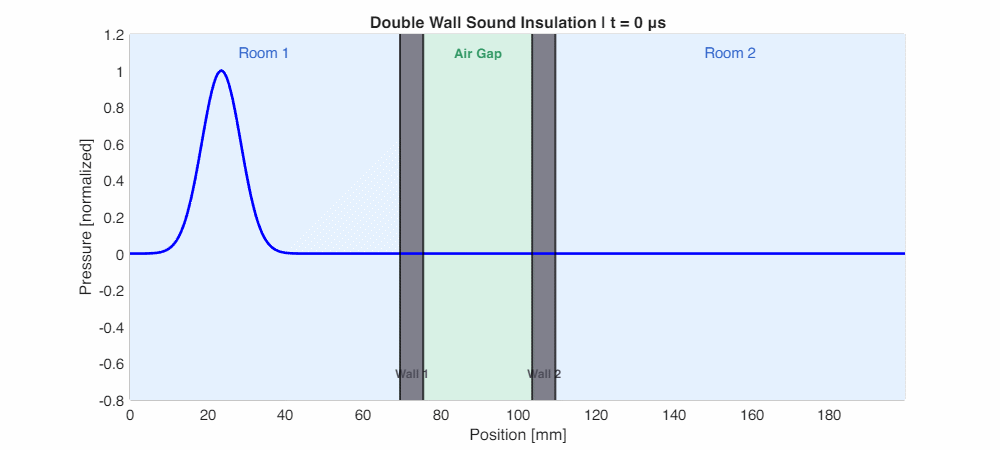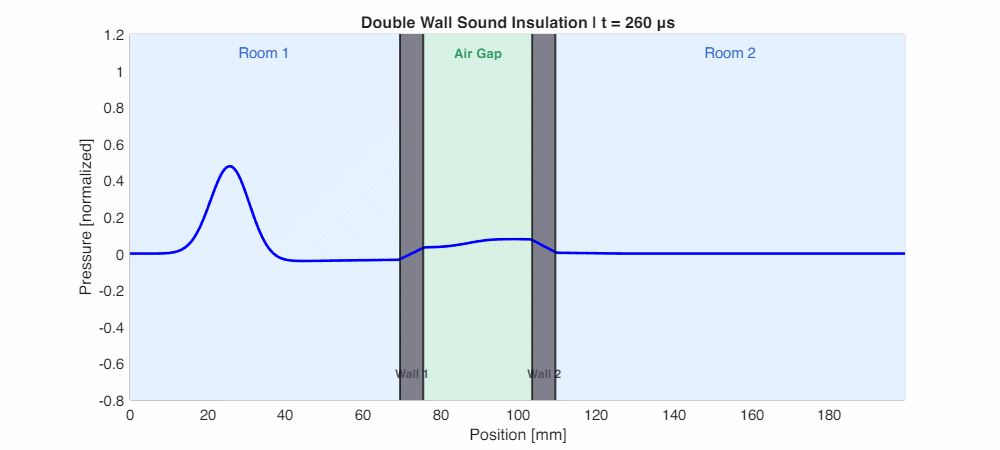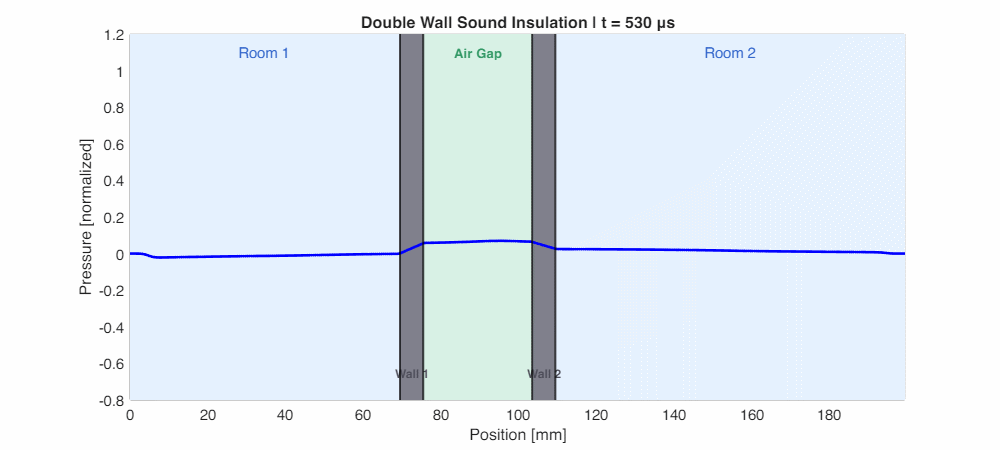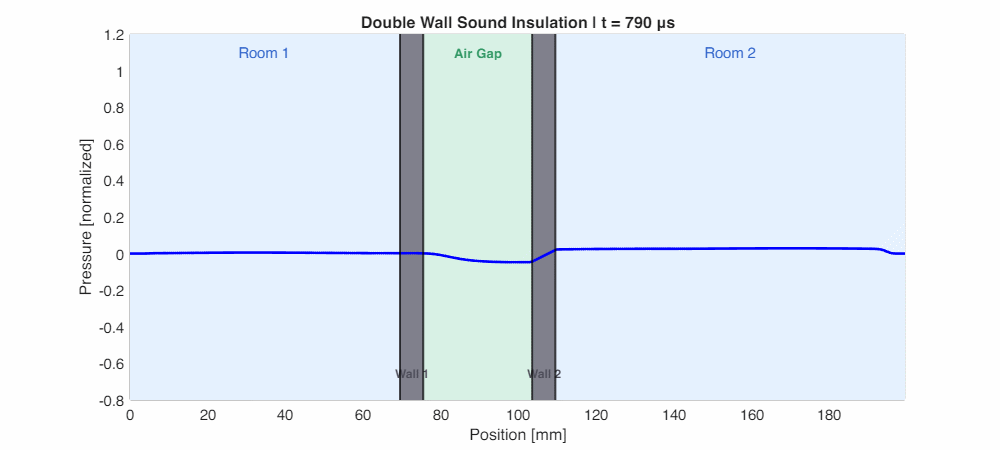
The Leaky Bucket: Sealing is Everything

You can build a concrete bunker with double walls, but if you leave a keyhole open, you might as well have used paper screens.

The engineering principle emphasizes the critical impact of leakage (holes and cracks) on sound insulation. Sound behaves like water under pressure; it forces itself through the path of least resistance.

• The Math of Leakage: If a wall has a transmission loss of 50 dB (blocking 99.999% of energy), but has a hole that takes up just 1% of the surface area, the total insulation drops to about 20 dB.
• Engineering Implication: In noise control engineering, applying sealant to cracks, using heavy gaskets on doors, and staggering electrical outlets in walls (so there isn’t a direct hole through the partition) is just as important as the wall material itself.

What’s Next?

We have blocked the sound with heavy walls and trapped it with double layers. But what if the sound is traveling inside a pipe, like the exhaust of a car or the ventilation of a building? We cannot block the pipe, or the air won’t flow.

In the next installment, “Mufflers – Reactive and Resistive Silencers,” we will explore how to let air pass while stopping sound, using expansion chambers and resistive silencing principles.

References:

• He Lin et al., Theoretical Acoustics and Engineering Applications, Science Press, 2006.