Learning Objectives

After reading this post, you will be able to:

• Understand the goal of association rule mining
• Know the key metrics: support, confidence, and lift
• Implement the Apriori algorithm for finding frequent itemsets
• Apply association rules to real-world market basket analysis

Theory

The Intuition: The Symbiosis Scouter

Imagine you are an ecologist exploring a vast Rainforest (The Dataset).

• Transaction: You examine small 10x10m patches of land.
• Itemset: The specific plants and animals you find in that patch.
• Association Rule: You notice a pattern: “Wherever I see a Clownfish, I see an Anemone.”

Association Rule Mining is about finding these Symbiotic Relationships in your data ecosystem, distinguishing true partnerships from random co-occurrences.

Applications:

• 🛒 Nature (Market): Clownfish & Anemone (Bread & Butter).
• 🌐 Web: Visited Page A & Page B.
• 🏥 Medicine: Symptom X & Disease Y.

Key Concepts

Support (How Common?)

• Analogy: “How many patches have both a Clownfish AND an Anemone?”
• Formula: $Support(A) = \frac{\text{Transactions with A}}{\text{Total Transactions}}$
• Goal: Filter out rare species. If a pair only appears once in 1,000 patches, it’s not a general rule.

Confidence (How Reliable?)

• Analogy: “If I see a Clownfish, how sure am I that an Anemone is also there?”
• Formula: $Confidence(A \rightarrow B) = \frac{Support(A \cup B)}{Support(A)}$
• Goal: Measure the strength of the implication.

Lift (True Symbiosis vs. Coincidence)

• Analogy: “Do they need each other? Or are they just both everywhere (like Ants and Grass)?”
• Formula: $Lift(A \rightarrow B) = \frac{Confidence(A \rightarrow B)}{Support(B)}$
• Interpretation:
  • Lift > 1 (Symbiosis): They appear together more than expected by chance. Positive correlation.
  • Lift = 1 (Independence): No relationship. (e.g., “People who buy Bread also breathe Air” - useless).
  • Lift < 1 (Competition): They avoid each other. Negative correlation.

The Apriori Algorithm

Apriori efficiently finds frequent itemsets using the apriori principle:

If an itemset is infrequent, all its supersets are also infrequent.

The Notion: “The Rotten Apple”

Think of a fruit basket.

• If one apple is rotten, the entire basket is considered “bad”.
• In Apriori: If {Beer} is rare (rotten), then {Beer, Diapers}, {Beer, Milk}, and {Beer, Anything} are also rare.
• Result: We don’t even bother checking the combinations. We throw the whole branch away.

This allows pruning of the search space.

Algorithm Steps:

1. Set minimum support threshold
2. Find frequent 1-itemsets
3. Generate candidate k+1 itemsets from frequent k-itemsets
4. Prune candidates with infrequent subsets
5. Count support and keep frequent ones
6. Repeat until no new itemsets found

Code Practice

Creating Transaction Data

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

import pandas as pd
import numpy as np

# Sample transaction data
transactions = [
    ['Bread', 'Milk'],
    ['Bread', 'Diapers', 'Beer', 'Eggs'],
    ['Milk', 'Diapers', 'Beer', 'Cola'],
    ['Bread', 'Milk', 'Diapers', 'Beer'],
    ['Bread', 'Milk', 'Diapers', 'Cola'],
    ['Bread', 'Milk', 'Beer'],
    ['Bread', 'Diapers', 'Cola'],
    ['Bread', 'Milk', 'Diapers', 'Eggs'],
    ['Milk', 'Diapers', 'Beer', 'Eggs'],
    ['Bread', 'Milk', 'Cola']
]

print("=" * 50)
print("TRANSACTION DATA")
print("=" * 50)
for i, t in enumerate(transactions[:5], 1):
    print(f"Transaction {i}: {t}")
print(f"... and {len(transactions)-5} more")

Output:

1
2
3
4
5
6
7
8
9

==================================================
TRANSACTION DATA
==================================================
Transaction 1: ['Bread', 'Milk']
Transaction 2: ['Bread', 'Diapers', 'Beer', 'Eggs']
Transaction 3: ['Milk', 'Diapers', 'Beer', 'Cola']
Transaction 4: ['Bread', 'Milk', 'Diapers', 'Beer']
Transaction 5: ['Bread', 'Milk', 'Diapers', 'Cola']
... and 5 more

Using mlxtend for Association Rules

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

# pip install mlxtend
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import apriori, association_rules

# Encode transactions
te = TransactionEncoder()
te_array = te.fit_transform(transactions)
df = pd.DataFrame(te_array, columns=te.columns_)

print("\n📊 Encoded transactions:")
print(df.head())

# Find frequent itemsets
# min_support=0.3: "Ignore species that appear in less than 30% of patches"
frequent_itemsets = apriori(df, min_support=0.3, use_colnames=True)
print(f"\n✅ Found {len(frequent_itemsets)} frequent itemsets")
print(frequent_itemsets.head(10))

Output:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

📊 Encoded transactions:
    Beer  Bread   Cola  Diapers   Eggs   Milk
0  False   True  False    False  False   True
1   True   True  False     True   True  False
2   True  False   True     True  False   True
3   True   True  False     True  False   True
4  False   True   True     True  False   True

✅ Found 18 frequent itemsets
   support                    itemsets
0      0.5           frozenset({Beer})
1      0.8          frozenset({Bread})
2      0.4           frozenset({Cola})
3      0.7        frozenset({Diapers})
4      0.3           frozenset({Eggs})
5      0.8           frozenset({Milk})
6      0.3    frozenset({Bread, Beer})
7      0.4  frozenset({Diapers, Beer})
8      0.4     frozenset({Beer, Milk})
9      0.3    frozenset({Cola, Bread})

Generating Association Rules

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

# Generate rules
# metric="confidence": "If A is present, B must be present at least 60% of the time"
rules = association_rules(frequent_itemsets, metric="confidence", min_threshold=0.6)
rules = rules.sort_values('lift', ascending=False)

print("\n" + "=" * 50)
print("ASSOCIATION RULES")
print("=" * 50)
print(f"\n📜 Found {len(rules)} rules with confidence ≥ 0.6\n")

# Display top rules
cols = ['antecedents', 'consequents', 'support', 'confidence', 'lift']
print(rules[cols].head(10).to_string())

Output:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

==================================================
ASSOCIATION RULES
==================================================

📜 Found 19 rules with confidence ≥ 0.6

                   antecedents                 consequents  support  confidence      lift
10           frozenset({Eggs})        frozenset({Diapers})      0.3        1.00  1.428571
13  frozenset({Diapers, Milk})           frozenset({Beer})      0.3        0.60  1.200000
16           frozenset({Beer})  frozenset({Diapers, Milk})      0.3        0.60  1.200000
1            frozenset({Beer})        frozenset({Diapers})      0.4        0.80  1.142857
8            frozenset({Cola})        frozenset({Diapers})      0.3        0.75  1.071429
15     frozenset({Milk, Beer})        frozenset({Diapers})      0.3        0.75  1.071429
2            frozenset({Beer})           frozenset({Milk})      0.4        0.80  1.000000
9            frozenset({Cola})           frozenset({Milk})      0.3        0.75  0.937500
7            frozenset({Milk})          frozenset({Bread})      0.6        0.75  0.937500
3            frozenset({Cola})          frozenset({Bread})      0.3        0.75  0.937500

Visualizing Rules

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

import matplotlib.pyplot as plt

fig, axes = plt.subplots(1, 2, figsize=(14, 6))

# Support vs Confidence
axes[0].scatter(rules['support'], rules['confidence'], 
                c=rules['lift'], cmap='viridis', s=100, alpha=0.7)
axes[0].set_xlabel('Support', fontsize=11)
axes[0].set_ylabel('Confidence', fontsize=11)
axes[0].set_title('Support vs Confidence', fontsize=12, fontweight='bold')
axes[0].grid(True, alpha=0.3)
plt.colorbar(axes[0].collections[0], ax=axes[0], label='Lift')

# Lift distribution
axes[1].barh(range(len(rules)), rules['lift'].values, color='steelblue', alpha=0.8)
axes[1].set_yticks(range(len(rules)))
axes[1].set_yticklabels([f"{list(a)} → {list(c)}" 
                         for a, c in zip(rules['antecedents'][:len(rules)], 
                                        rules['consequents'][:len(rules)])], fontsize=8)
axes[1].set_xlabel('Lift', fontsize=11)
axes[1].set_title('Rules by Lift', fontsize=12, fontweight='bold')
axes[1].axvline(x=1, color='r', linestyle='--', label='Lift = 1')
axes[1].legend()
axes[1].grid(True, alpha=0.3, axis='x')

plt.tight_layout()
plt.savefig('assets/association_rules.png', dpi=150)
plt.show()

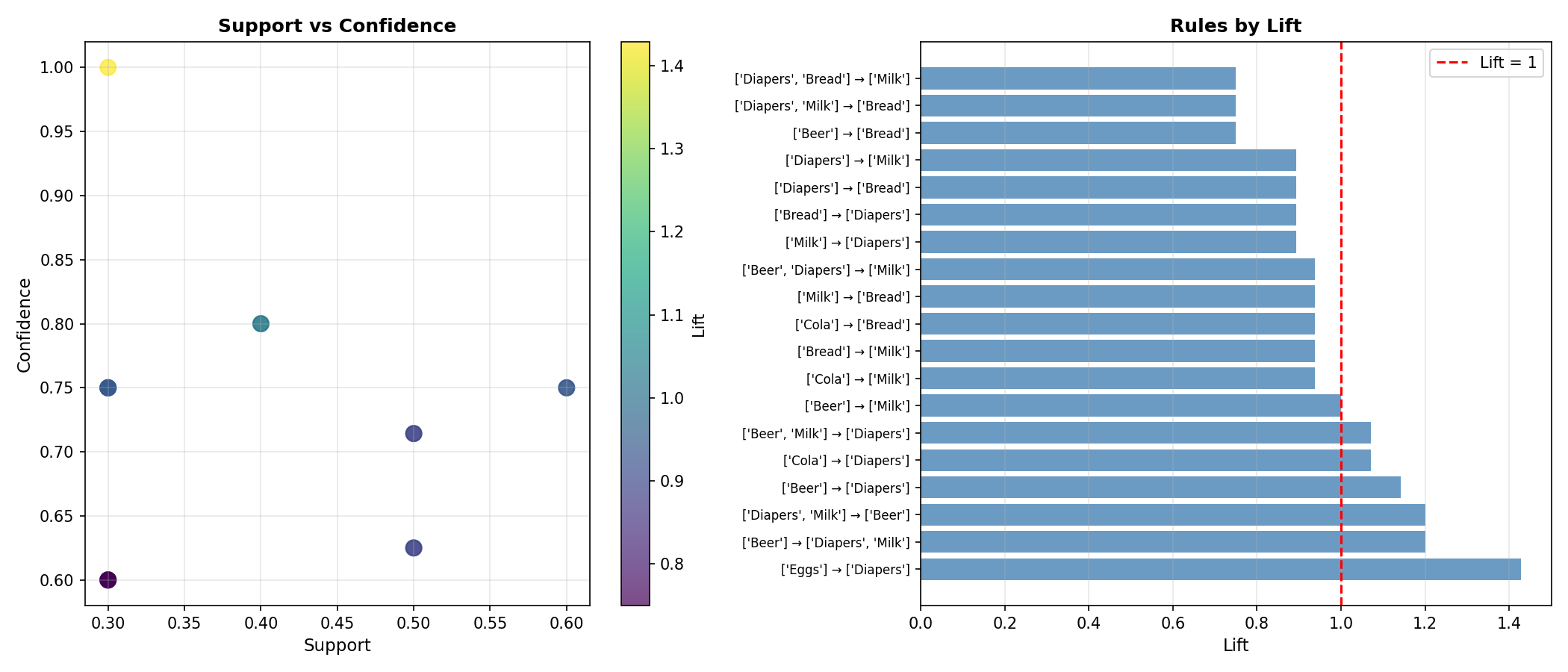
Deep Dive

Interpreting Metrics

The Popularity Trap (Confidence vs. Lift)

Why isn’t Confidence enough? Imagine a supermarket where everyone buys Water (Support = 90%).

• Rule: {Bread} -> {Water}
• Confidence: 90% (Wow! High reliability!)
• Reality: It’s useless. They would have bought Water anyway.

Lift exposes the truth:

• If Lift = 1, the rule is just a coincidence.
• Analogy: “Breathing Air” has 100% confidence with “Buying Bread”, but zero predictive value. Lift detects this independence.

Limitations and Challenges

Challenges in association rule mining:

1. Combinatorial explosion: Many possible itemsets
2. Threshold selection: min_support and min_confidence affect results
3. Spurious patterns: High support doesn’t mean meaningful
4. Scalability: Large transaction databases are expensive

Alternatives to Apriori

Summary

References

• Agrawal, R. & Srikant, R. (1994). “Fast Algorithms for Mining Association Rules”
• mlxtend Documentation
• “Data Mining: Concepts and Techniques” by Han, Kamber & Pei - Chapter 6