Tensors: AI vs. Physics - Same Name, Different Worlds
If you’ve ever wondered why the same word “tensor” appears in both a PyTorch tutorial and a general relativity textbook, you’re not alone. While AI practitioners use tensors to store and manipulate data efficiently, physicists rely on them to describe the fabric of spacetime and the forces within materials. This article explores these two seemingly different worlds—and reveals both their distinctions and surprising connections.
At a Glance: Two Worlds Compared
| Aspect | Tensor in AI/ML | Tensor in Physics/Mechanics |
|---|---|---|
| Definition | Multi-dimensional array of numbers | Geometric object with transformation rules |
| Key Property | Shape and data type | Covariance/Contravariance under coordinate change |
| Notation | tensor.shape = (3, 4, 5) | $T^{ij}{}_k$ with indices |
| Primary Use | Data container for computation | Describing physical quantities invariantly |
| Transformation | Arbitrary reshaping allowed | Must follow strict tensor transformation laws |
| Popular Framework | PyTorch, TensorFlow, NumPy | Einstein notation, Differential geometry |
Tensor in AI/Deep Learning
What It Means
In the world of AI and deep learning, a tensor is essentially a multi-dimensional array—a natural generalization of scalars, vectors, and matrices extended to any number of dimensions. Think of it as the fundamental data structure that powers modern neural networks.
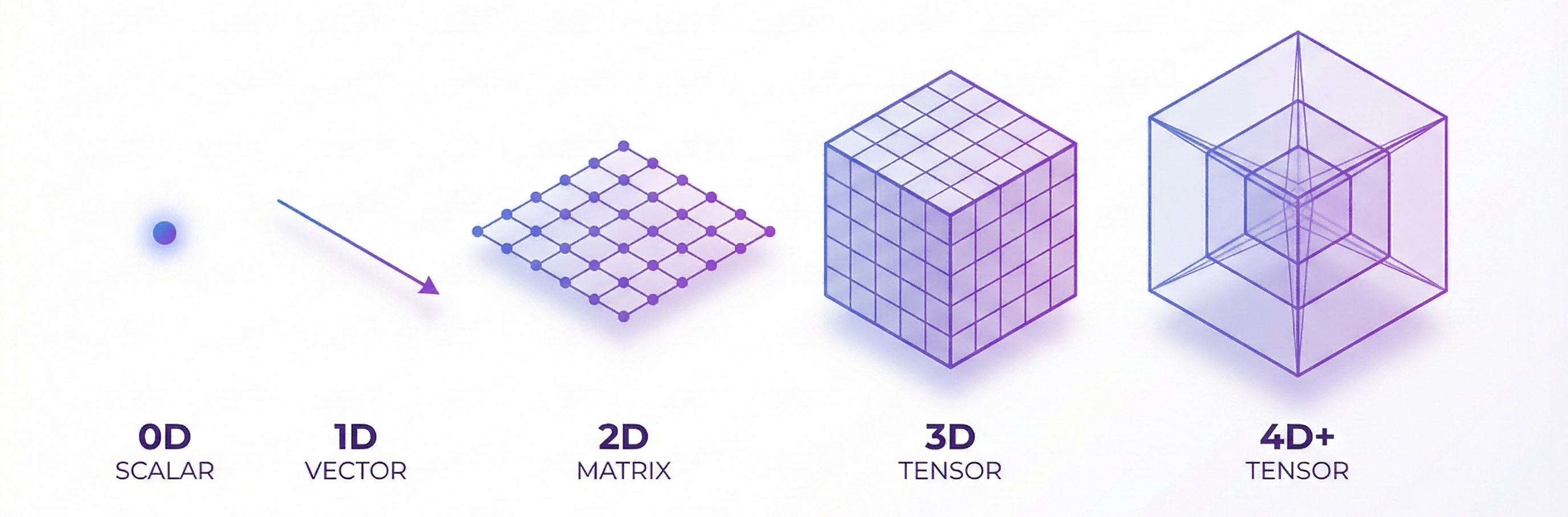
Example in PyTorch
| |
Key Characteristics
| Property | Description |
|---|---|
| Shape | Tuple of dimensions, e.g., (batch, channels, H, W) |
| dtype | Data type: float32, int64, bool, etc. |
| Device | CPU or GPU memory location |
| Requires Gradient | Whether to track gradients for backpropagation |
| Contiguity | Memory layout (row-major vs column-major) |
Why the Name “Tensor”?
The term was borrowed from mathematics and physics, but with a simplified interpretation:
- In AI, tensors are essentially sophisticated arrays optimized for GPU computation
- There is no requirement for coordinate transformation invariance
- The name primarily emphasizes the concept of “generalized multi-dimensional data”
Tensor in Physics/Mechanics
What It Means
In physics and mechanics, a tensor takes on a deeper meaning. It is a geometric object that describes physical quantities and transforms predictably under coordinate changes.
A tensor is not merely an array of numbers—it is fundamentally defined by how it transforms.
The Essence: Transformation Rules
When coordinates change from $x^i$ to $x’^i$, tensor components transform as:
Contravariant (upper index): $$V’^i = \frac{\partial x’^i}{\partial x^j} V^j$$
Covariant (lower index): $$V’_i = \frac{\partial x^j}{\partial x’^i} V_j$$
Mixed tensor example (rank-2): $${T’}^i_j = \frac{\partial x’^i}{\partial x^k} \frac{\partial x^l}{\partial x’^j} T^k_l$$
Tensor Ranks in Physics
| Rank | Example | Physical Meaning |
|---|---|---|
| 0 | Temperature $T$ | Scalar - same in all coordinate systems |
| 1 | Velocity $v^i$ | Vector - direction and magnitude |
| 2 | Stress tensor $\sigma^{ij}$ | Describes internal forces in materials |
| 3 | Piezoelectric tensor | Electro-mechanical coupling |
| 4 | Elasticity tensor $C^{ijkl}$ | Relates stress to strain |
The Stress Tensor: A Classic Example
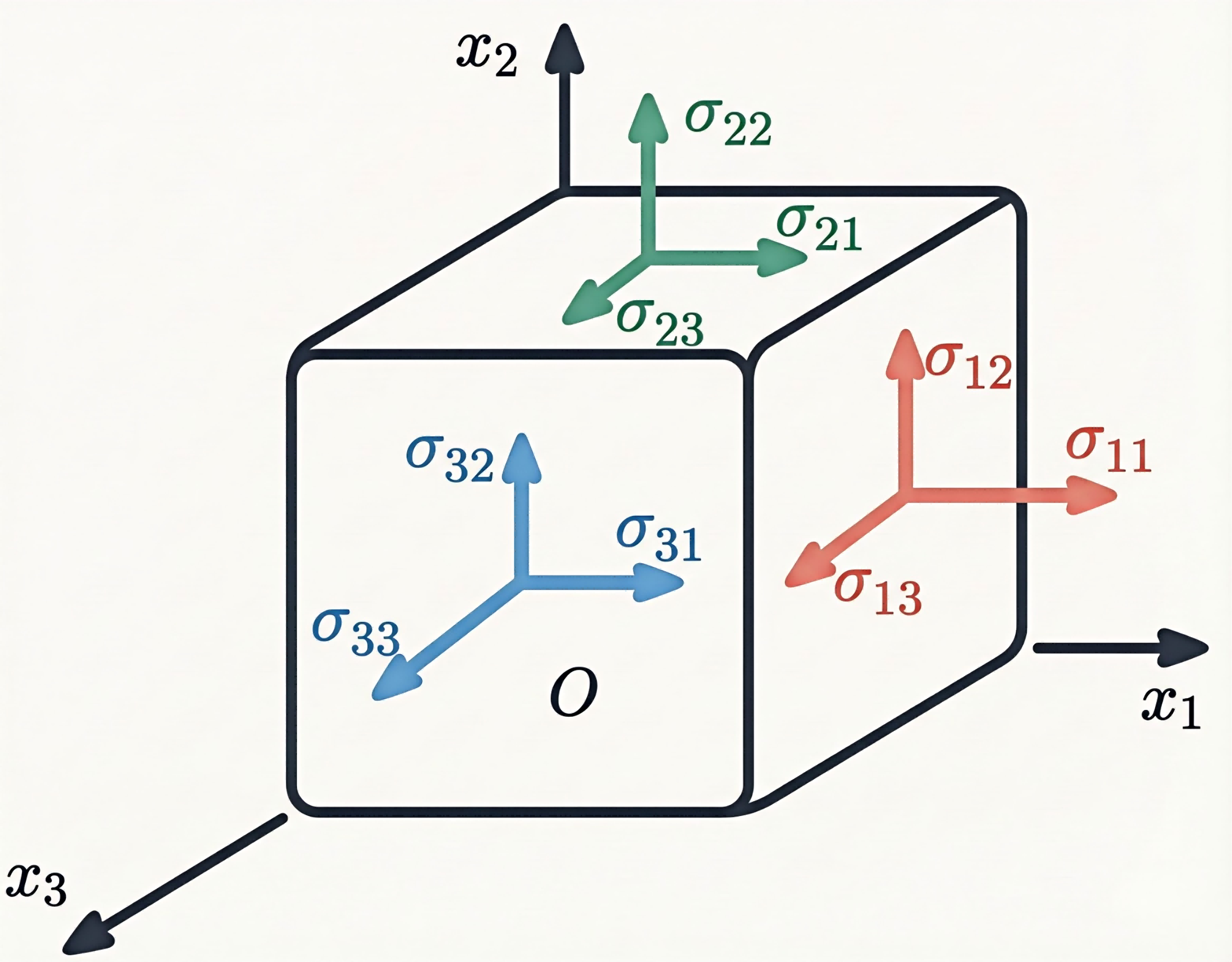
The stress tensor is a quintessential rank-2 tensor in mechanics:
$$\sigma = \begin{pmatrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{pmatrix}$$
What makes this tensor particularly instructive:
- It describes the internal forces acting at any point within a material
- Its components change when you rotate the coordinate system
- Yet the underlying physical reality—the forces themselves—remains unchanged
- This transformation invariance is precisely what makes it a true tensor
Einstein Summation Convention
Physicists use compact notation:
$$T^{ij} = A^i B^j \quad \text{(outer product)}$$
$$v^i = g^{ij} v_j \quad \text{(index raising with metric)}$$
$$T^i{}_i = T^1{}_1 + T^2{}_2 + T^3{}_3 \quad \text{(trace - implicit sum)}$$
The Key Differences
Now that we’ve seen both interpretations, let’s examine what truly sets them apart.
Transformation Behavior
graph TB
subgraph AI["AI Tensor"]
A1["Can reshape freely"]
A2["transpose, view, reshape"]
A3["No coordinate system attached"]
end
subgraph Physics["Physics Tensor"]
P1["Must follow transformation laws"]
P2["Covariant/Contravariant indices"]
P3["Coordinate-independent meaning"]
end
In AI, reshaping is routine:
In Physics, on the other hand, reshaping a stress tensor arbitrarily would completely destroy its physical meaning!
Index Semantics
| Aspect | AI Tensor | Physics Tensor |
|---|---|---|
| Indices | Just array dimensions | Contravariant ($T^i$) or covariant ($T_i$) |
| Contraction | torch.einsum('ij,jk->ik', A, B) | $A^i_j B^j_k = C^i_k$ |
| Meaning | Positional access | Transformation behavior |
When They Align
Despite differences, there are overlaps:
| Operation | AI Code | Physics Notation |
|---|---|---|
| Matrix multiply | A @ B | $A^i_{\ j} B^j_{\ k}$ |
| Dot product | torch.dot(a, b) | $a_i b^i$ |
| Outer product | torch.outer(a, b) | $a^i b^j$ |
| Trace | torch.trace(A) | $A^i_{\ i}$ |
| Transpose | A.T | $A_{ji}$ from $A_{ij}$ |
Practical Takeaways
For AI/ML Practitioners
When you encounter “tensor” in a deep learning context:
- Think of it as a multi-dimensional array
- Focus on shapes, broadcasting, and GPU acceleration
- Coordinate transformations are not your concern
For Physicists/Engineers
When encountering a physical tensor:
- Think transformation invariance
- Track index positions (up vs down)
- Remember the metric tensor for raising/lowering indices
Bridging Both Worlds
If your work involves Physics-Informed Neural Networks (PINNs) or scientific machine learning:
- You will likely need both perspectives!
- For example: learning stress fields requires respecting tensor transformation symmetries
- Libraries such as
Equivariant Neural Networksare specifically designed to enforce physical tensor properties within AI models
Summary
| Question | AI Tensor | Physics Tensor |
|---|---|---|
| “What is it?” | Multi-dimensional array | Geometric object |
| “What defines it?” | Shape and dtype | Transformation rules |
| “Why this name?” | Generalization of matrices | Mathematical entity with invariance |
| “Key skill needed?” | Array manipulation, GPU coding | Differential geometry, index notation |
| “Can I reshape freely?” | Yes | No - must preserve tensor laws |
The Bottom Line:
- In AI: A tensor is a sophisticated array optimized for efficient computation
- In Physics: A tensor is a geometric entity defined by its coordinate invariance
- Same word, different meanings—but both are absolutely essential in their respective domains!
References
- Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.
- Misner, C. W., Thorne, K. S., & Wheeler, J. A. (1973). Gravitation. W.H. Freeman.
- PyTorch Documentation - Tensors
- Wikipedia - Tensor (Physics)
- 3Blue1Brown - Tensors for Beginners