In our previous installment, we watched sound waves bounce off hard walls and travel down pipes. We learned that when sound hits a rigid boundary, most of its energy reflects back. This causes echoes in concert halls and deafening noise in factories.

To create a quiet environment, we need to make sound disappear. But the First Law of Thermodynamics tells us energy cannot be destroyed, only converted. So, how do we turn the kinetic energy of a sound wave into something harmless, like heat?

In this fourth post, we explore the two primary mechanisms of acoustic absorption: the friction of porous materials and the “springs” of resonance.

The Sponge Effect: Porous Materials

When you think of soundproofing, you probably imagine foam, fiberglass, or thick curtains. These are porous materials.

But here’s a puzzle: a solid block of soft rubber actually reflects sound quite well. So “softness” alone isn’t the answer. The real magic lies in the structure—a network of tiny, interconnected pores that allow air to flow into the material. Without this internal access, the sound wave just bounces off.

The Mechanism: Friction and Viscosity

When a sound wave hits a porous material, the air molecules are forced to vibrate back and forth inside these tiny, narrow channels.

• Viscous Losses: As air moves through these capillaries, viscosity creates friction between the air particles and the pore walls. This friction converts the ordered vibrational energy of sound into random thermal energy (heat).
• Thermal Losses: Additionally, the compression and rarefaction of the air generate minute temperature changes. Heat flows from the air to the fibers of the material, causing further energy loss.
• Flow Resistivity ($\sigma$): The key design parameter for porous absorbers is flow resistivity—how much a material resists airflow per unit thickness (units: $\text{Pa} \cdot \text{s/m}^2$). Too low, and air passes through without friction; too high, and the sound reflects off the surface. Optimal values are typically 10,000–50,000 $\text{Pa} \cdot \text{s/m}^2$.

The Thickness Problem: Why Bass Is Hard

Here’s the catch: for friction to work, air must move. But what happens near a rigid wall?

Think of it this way: air particles can’t pass through the wall, so they pile up and bounce back. Right at the surface, air velocity is essentially zero—all the energy is in pressure, not motion. The maximum air motion happens not at the wall, but at a distance of λ/4 away from it.

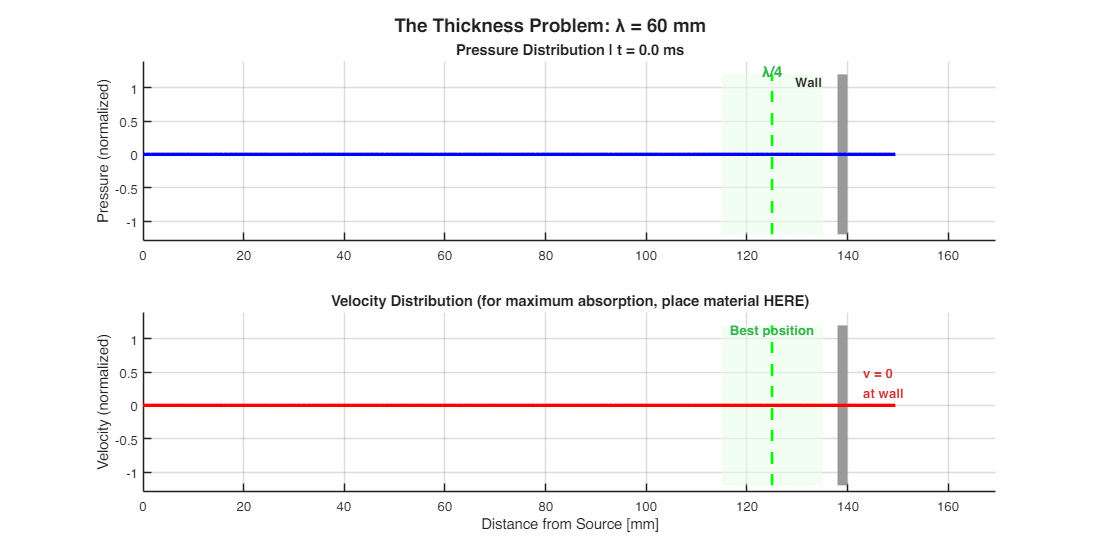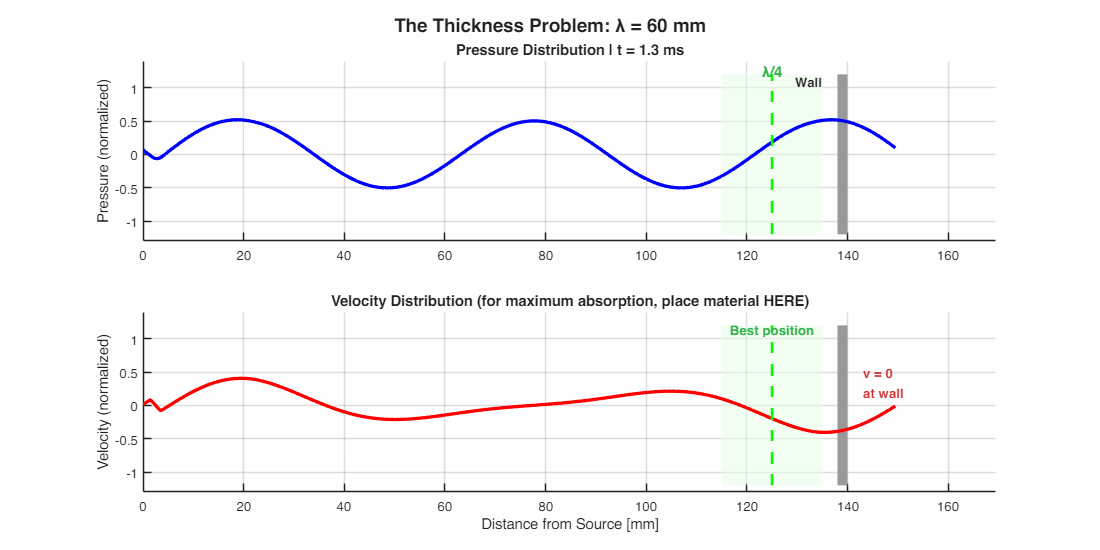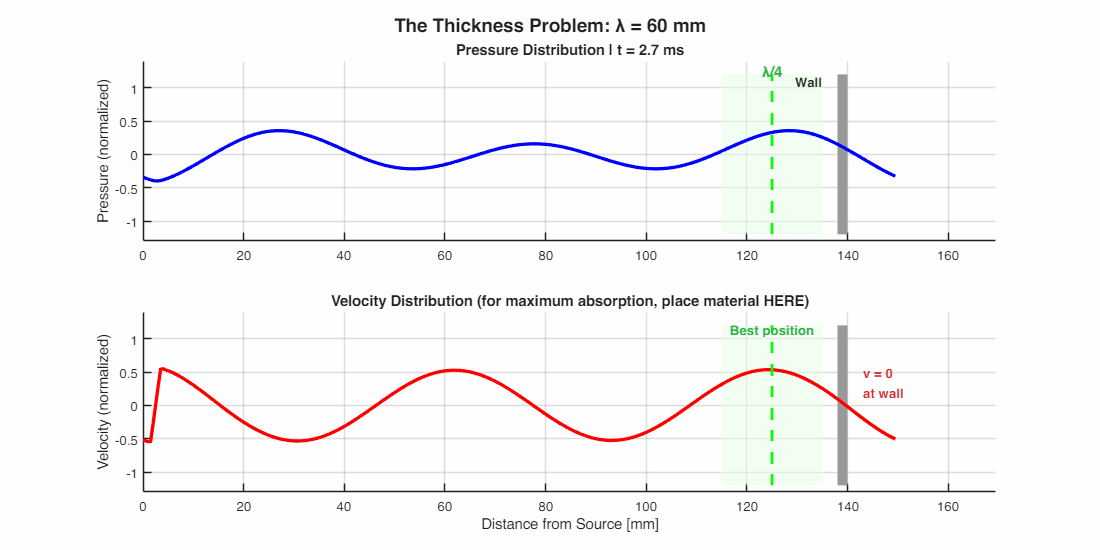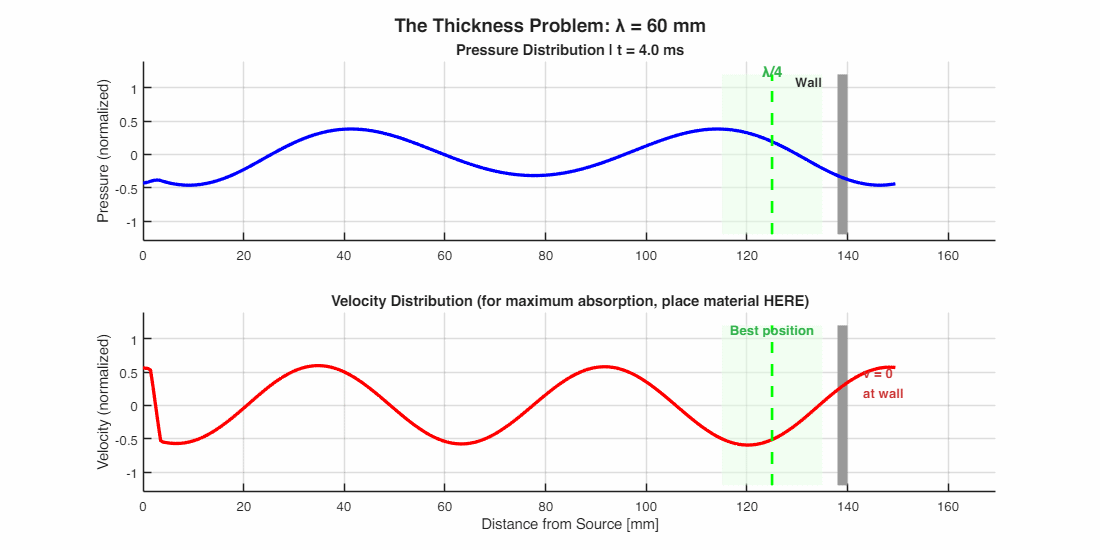
This creates a design headache. A thin foam panel stuck directly on a wall sits right where air isn’t moving—so it absorbs almost nothing. To catch a 100 Hz bass tone (wavelength ≈ 3.4 m), you’d need material 85 cm thick, or mount a thinner layer on standoffs to position it at the velocity maximum.

Concert halls use heavy drapes; studios mount panels on air gaps. But for really deep bass, porous materials become impractically bulky. We need a completely different approach.

The Bottle Effect: Helmholtz Resonators

Porous materials excel at absorbing high-pitched sounds, but they become impractically bulky for low-frequency rumble. Enter resonance absorption—a completely different strategy that uses physics instead of thickness.

You’ve experienced this yourself: blow across the top of an empty bottle, and it produces a deep “whoooo” at a specific pitch. That bottle is a Helmholtz Resonator. Used in reverse, it can trap sound instead of making it.

Why Does It Work?

The physics is beautifully simple—it’s just a mass on a spring:

• The Mass: The plug of air in the narrow neck moves as a unit when pushed.
• The Spring: The large cavity volume acts like a pneumatic cushion—compress it, and it pushes back.

This system has a natural frequency, just like a guitar string:

$$ f_0 = \frac{c}{2\pi}\sqrt{\frac{S}{V \cdot l_{eff}}} $$

where $S$ is the neck area, $V$ is the cavity volume, $l_{eff}$ is the effective neck length, and $c$ is the speed of sound. For a typical wine bottle ($V \approx 750$ mL, neck $\varnothing 2$ cm, length 5 cm), this gives $f_0 \approx 100$ Hz—a deep bass tone.

The Sound Trap

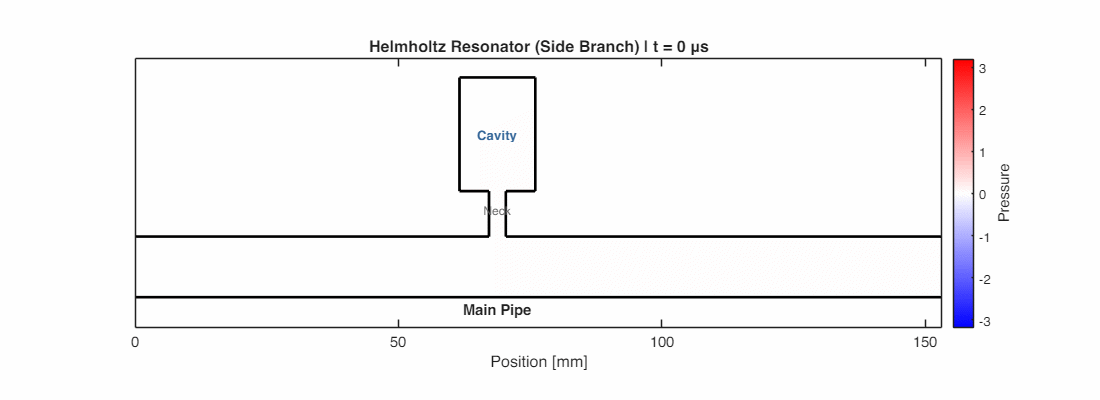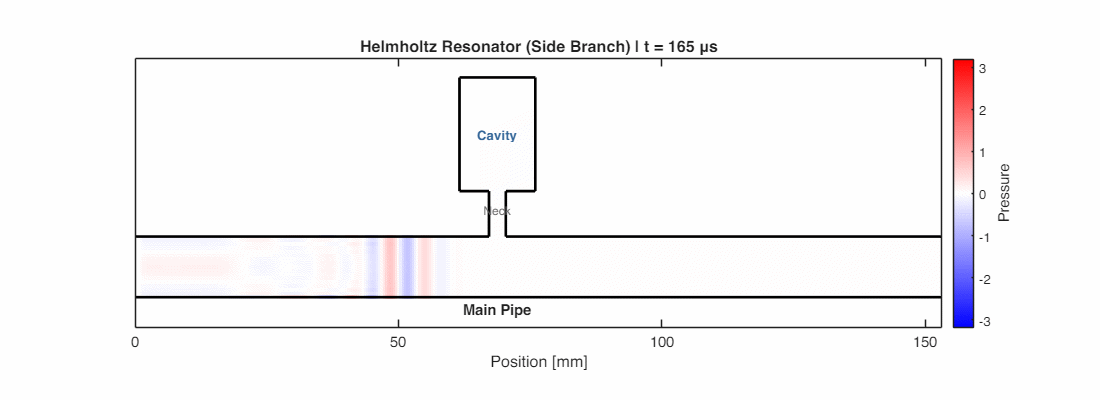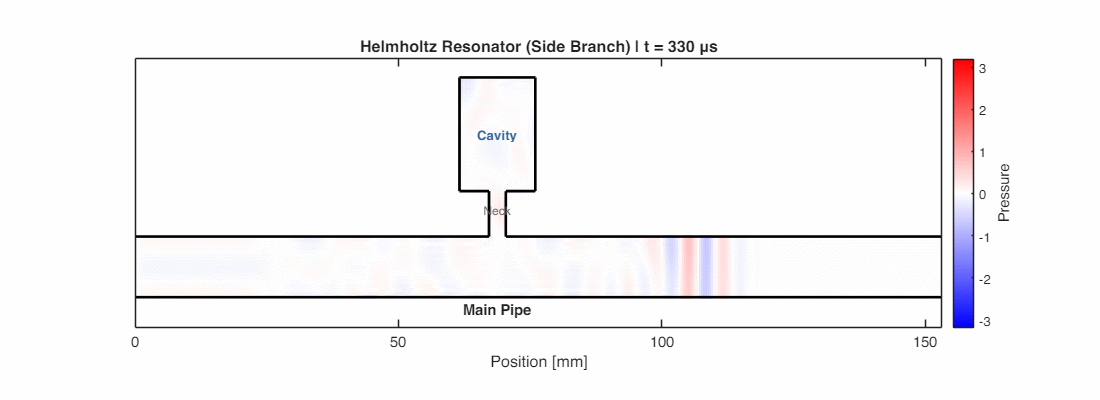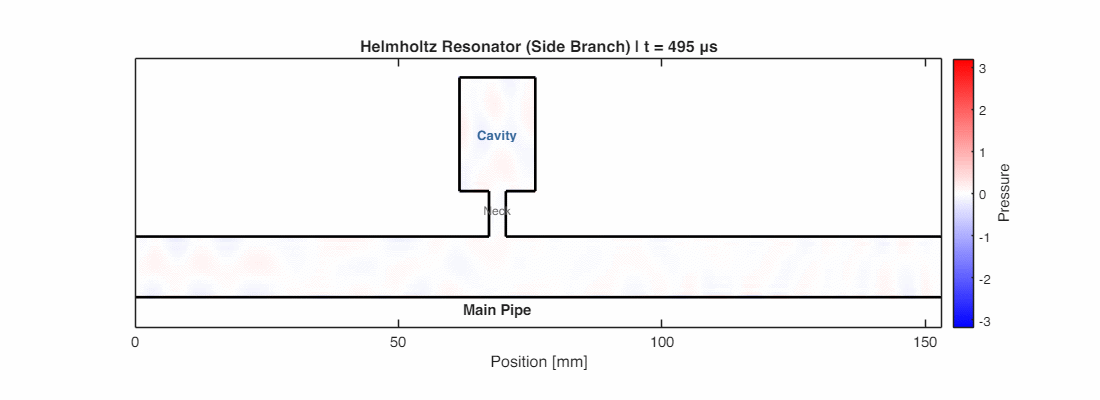
When sound at the resonator’s natural frequency passes by, the air plug oscillates violently—the resonator acts like a “sound sink,” greedily absorbing energy from the field.

In electrical terms, it’s an LC circuit: the neck is an inductor (storing kinetic energy in moving air), and the cavity is a capacitor (storing potential energy in compressed air). At resonance, energy sloshes between them, creating a “short circuit” for that specific frequency. Friction in the neck gradually converts this trapped energy to heat.

This makes Helmholtz resonators perfect for targeting specific booming tones—car mufflers, HVAC ducts, and concert hall linings all exploit this principle.

Engineering Silence: Wedges and Composites

In advanced engineering, these two principles are often combined.

• Anechoic Wedges: If you have seen photos of “dead rooms” (anechoic chambers) used for testing microphones, you have seen walls covered in deep, sharp wedges. These wedges provide a gradual impedance transition from air ($Z = 415$ Rayls) to the absorptive core. By slowly increasing the material density, reflections are minimized—the wave is “eased” into the absorber rather than bouncing off its face. Wedge depth is typically $\lambda/4$ of the lowest target frequency.

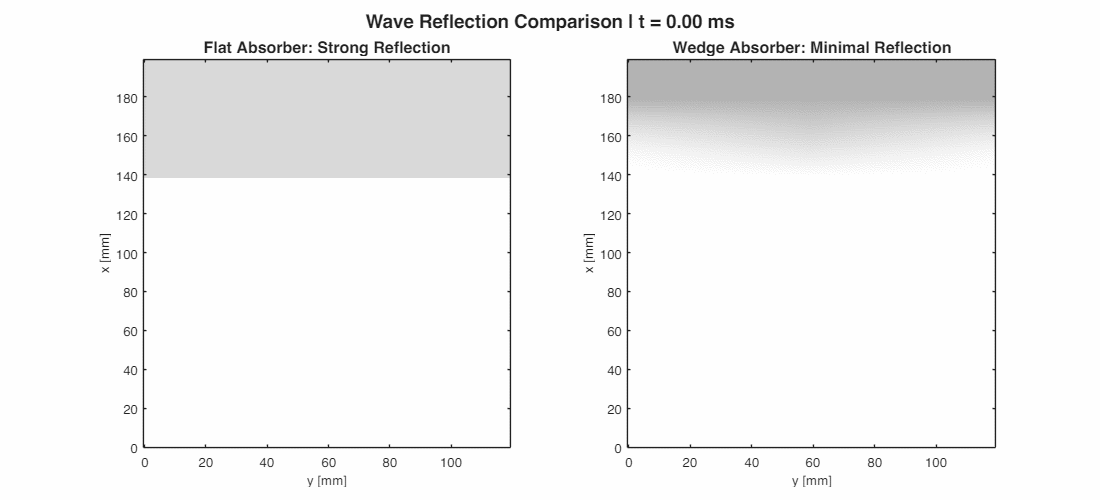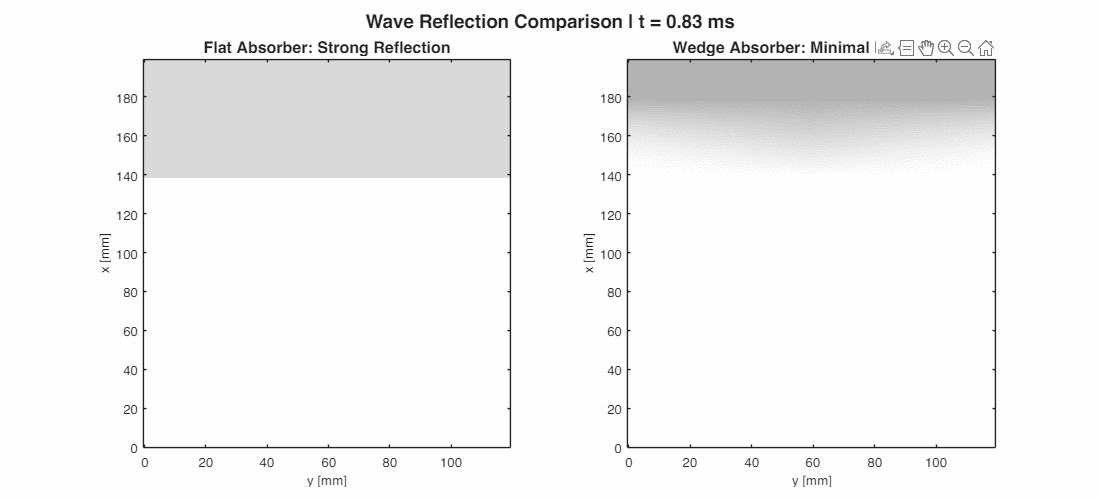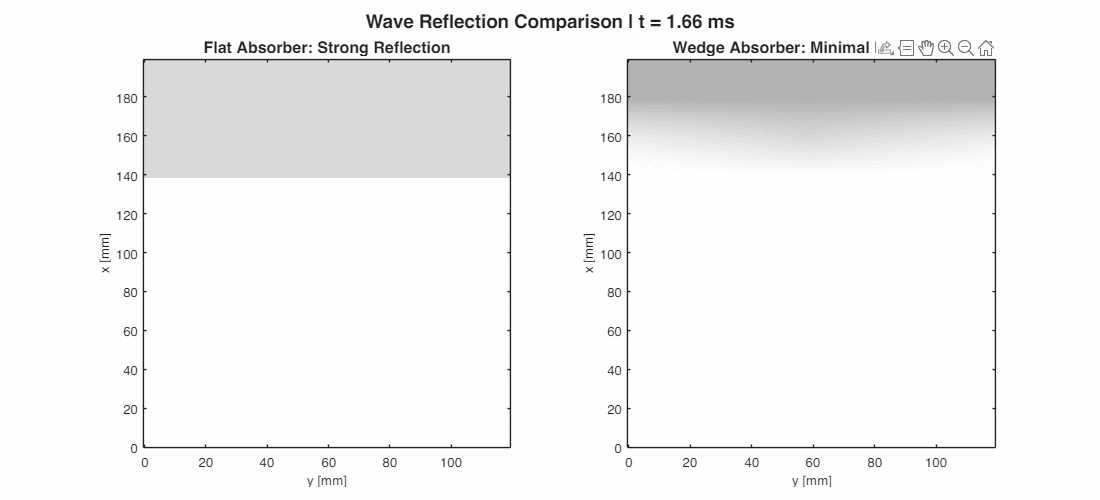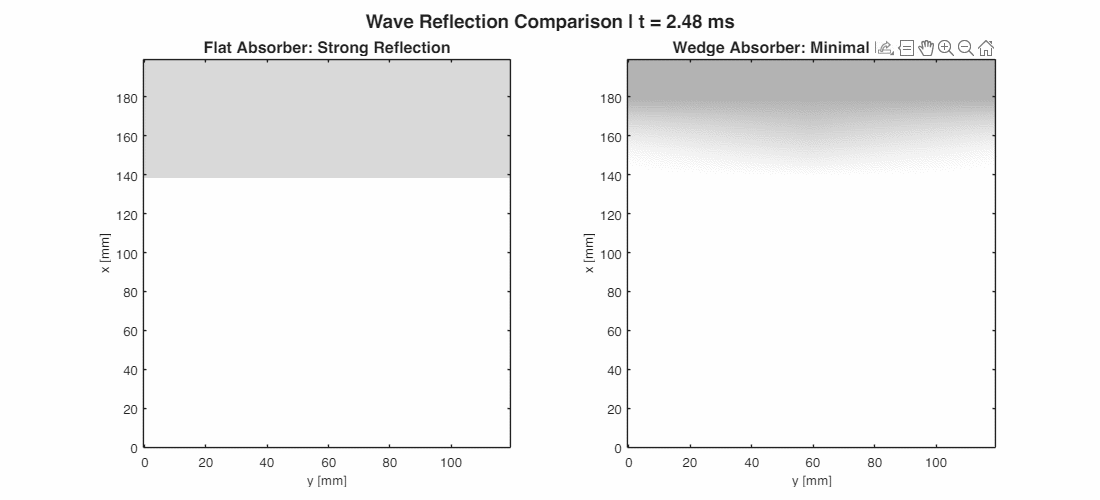
• Perforated Panels: In offices and gyms, you often see metal sheets with little holes. These aren’t just for decoration. The holes act as the “necks” of Helmholtz resonators, and the airspace behind them acts as the “cavity.” Often, porous material is placed behind the holes to broaden the frequency range of absorption.

What’s Next?

We’ve now seen two strategies: porous materials (friction in fibers) and resonators (tuned cavities). But porous materials can be dirty and fragile, and resonators are narrow-band—great for one frequency, useless for others.

The perforated panels we just discussed use large holes (several mm) that create Helmholtz resonators. But what if we made the holes much smaller—sub-millimeter? At that scale, something different happens: the air itself experiences significant viscous friction inside the hole, not in a cavity behind it.

In the next installment, “Absorption II – Micro-Perforated Panels,” we will explore one of the most elegant contributions of Chinese acoustics: the Micro-Perforated Panel (MPP) theory developed by Maa Dayou. We’ll see how drilling holes smaller than a millimeter can turn a clean, durable metal sheet into a broadband sound absorber—no fibers, no fragile foam.

References:

• He Lin et al., Theoretical Acoustics and Engineering Applications, Science Press, 2006.
• Ma Dayou, Modern Acoustics Theory Basis, Science Press, 2004.