Acoustics-03: Propagation – Reflection, Refraction, and Ducts
In the first two parts of this series, we defined sound as a physical wave and explored how our ears perceive it. But sound rarely travels through an infinite, empty void. In the real world, sound hits walls, squeezes through pipes, and leaks through cracks.
Today, we track the journey of a wave. We will explore why sound bounces, how it behaves in a “highway” (duct), and the strange phenomenon where waves stand still.
The Great Barrier: Reflection and Refraction
When a sound wave traveling in one medium (like air) hits a different medium (like a concrete wall or water), it doesn’t just stop. It splits. Part of the energy bounces back (reflection), and part of it keeps going (transmission).
But what decides how much bounces and how much goes through? The answer lies in Impedance Matching.
The Law of Impedance
The behavior at a boundary is dictated by the Characteristic Impedance ($Z = \rho c$), which is the product of the medium’s density ($\rho$) and the speed of sound ($c$) inside it.
Why $\rho c$? Impedance measures how much “push-back” a medium offers to a wave. When a sound wave compresses a region, it imparts momentum to the particles. The rate of momentum transfer per unit area, per unit particle velocity, is exactly $\rho c$. A denser medium ($\rho \uparrow$) or a stiffer one ($c \uparrow$) resists acoustic motion more strongly.
The Reflection Coefficient
When a wave hits a boundary head-on (normal incidence), some energy reflects back and some transmits through. The ratio of reflected to incident pressure is the reflection coefficient:
$$ r_p = \frac{Z_2 - Z_1}{Z_2 + Z_1} $$
where $Z_1$ and $Z_2$ are the impedances of the two media. This single formula governs all reflection behavior. Let’s explore its three limiting cases:
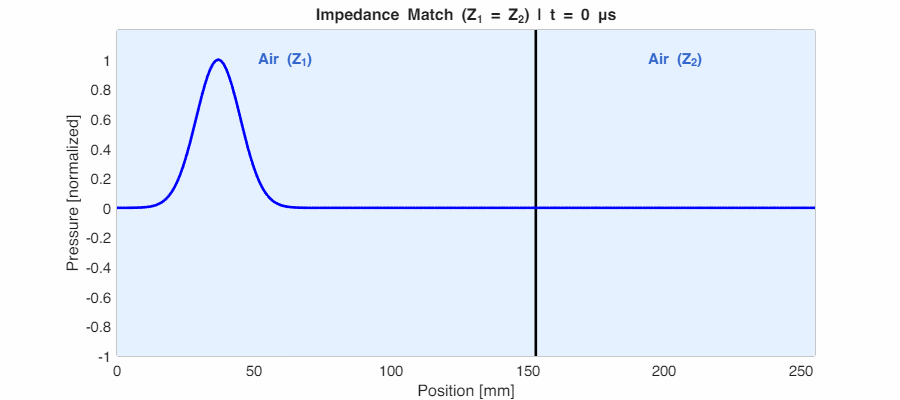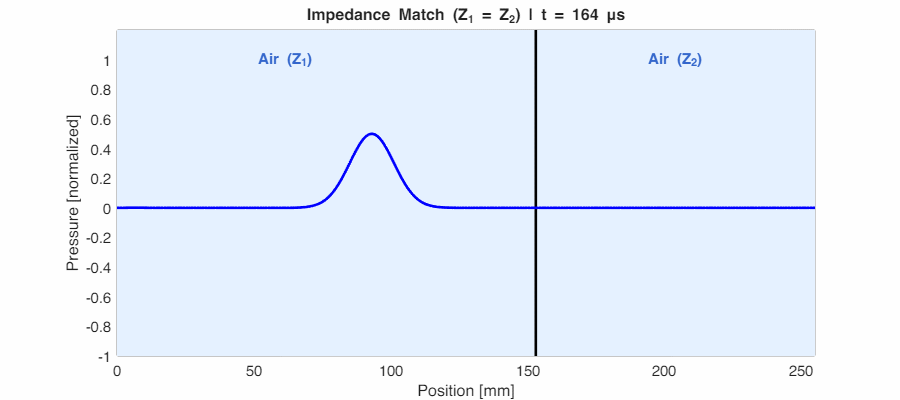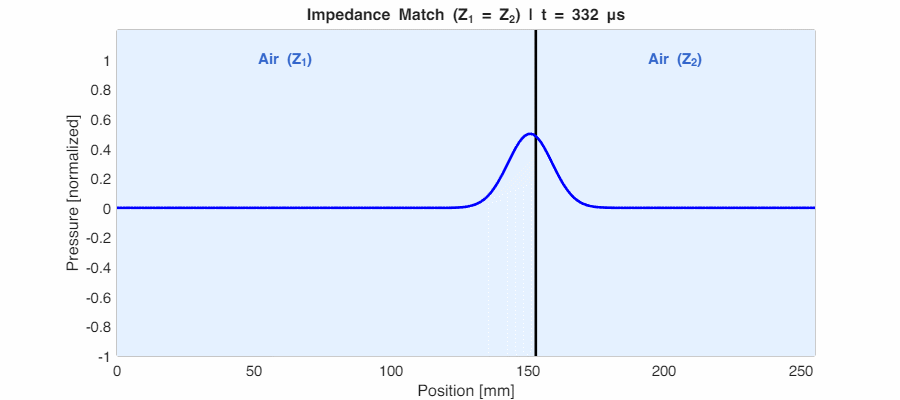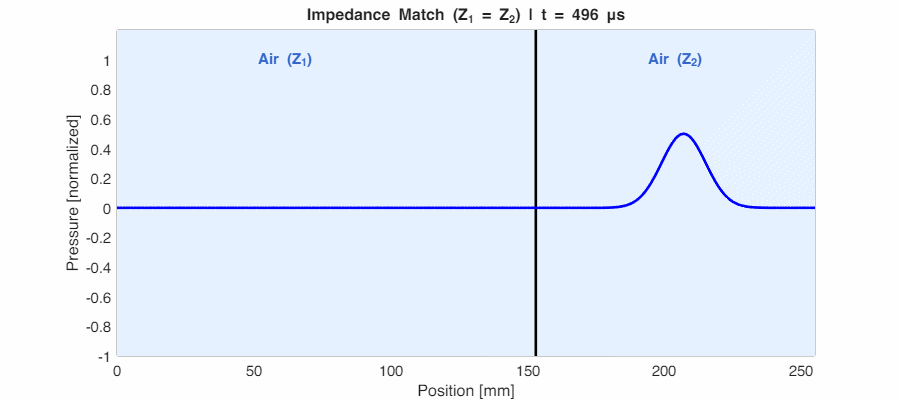
Case 1: Impedance Match ($Z_1 = Z_2$) → $r_p = 0$
When the impedances are identical, the reflection is zero. The boundary is acoustically “invisible”—the wave passes through as if nothing were there. This is the principle behind impedance matching in audio engineering.
Case 2: Hard Boundary ($Z_2 \gg Z_1$) → $r_p \approx +1$
If the second medium is much denser (like sound hitting a concrete wall from air), $r_p$ approaches +1. Almost all energy reflects back, and the reflected wave is in phase with the incident wave (peaks stay as peaks).
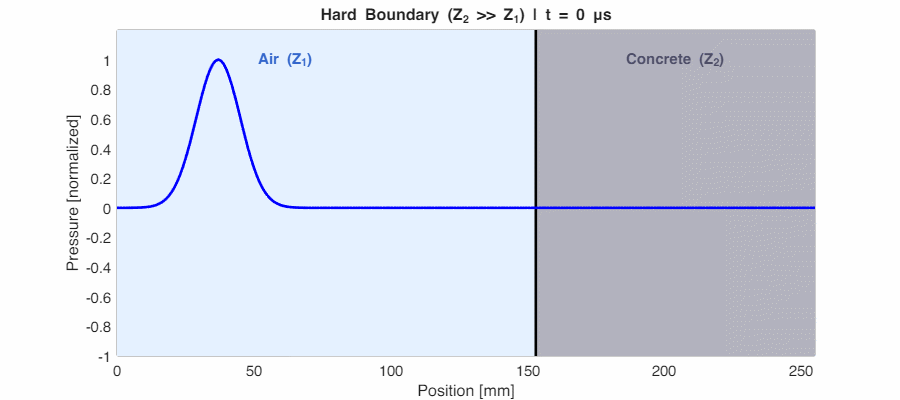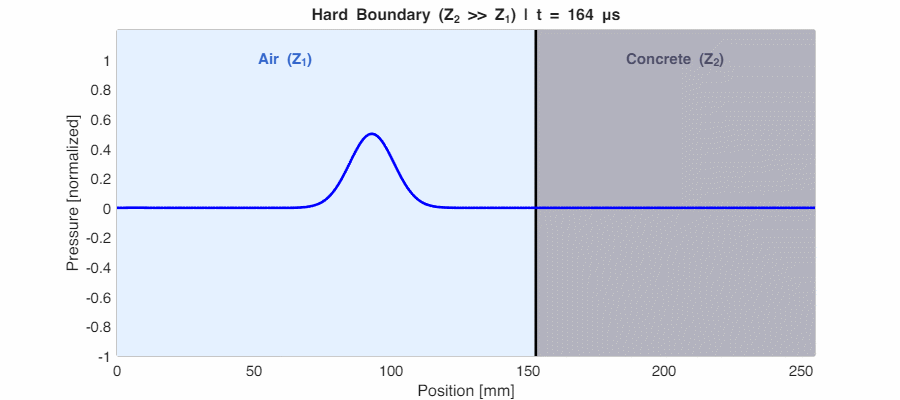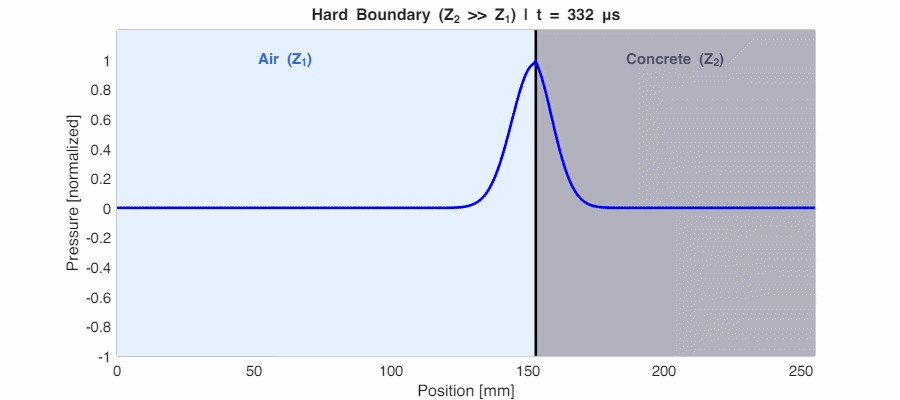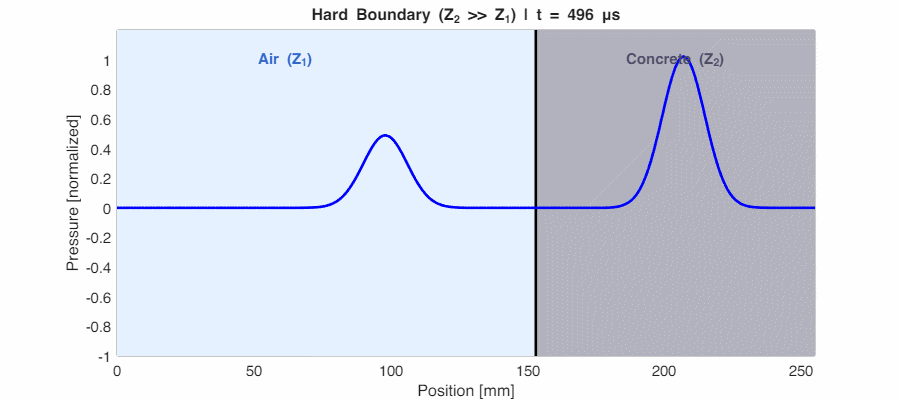
Why is the transmitted pressure higher than the incident pressure?
In the animation above, the wave inside concrete appears taller than the incident wave. This is physically correct! The pressure transmission coefficient is $t_p = \frac{2Z_2}{Z_1 + Z_2}$, which can exceed 1 when $Z_2 > Z_1$.
However, energy is still conserved. Power = Pressure × Velocity. In high-impedance materials, particle velocity is very low, so despite higher pressure, very little energy actually transmits. It’s like pushing against a wall—the wall experiences high force but barely moves, so minimal work is done.
Case 3: Soft Boundary ($Z_2 \ll Z_1$) → $r_p \approx -1$
If the second medium is much lighter (like sound hitting a foam surface), $r_p$ approaches -1. Energy still reflects strongly, but the wave is phase-inverted—peaks become troughs. This 180° shift is the signature of a “soft” or “pressure-release” boundary.
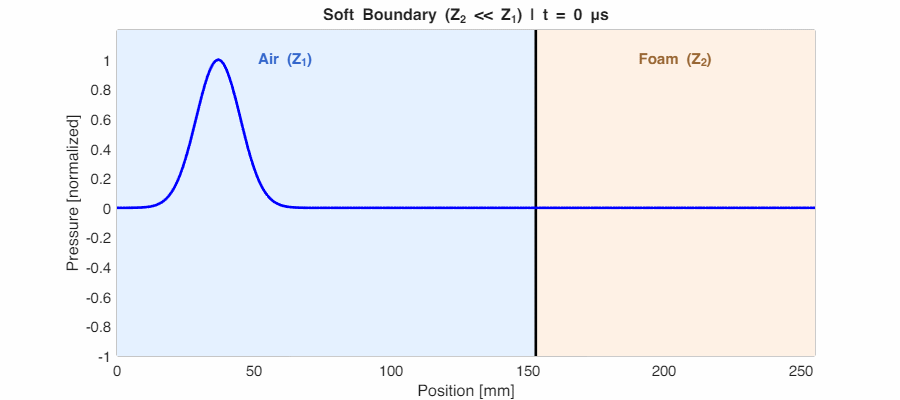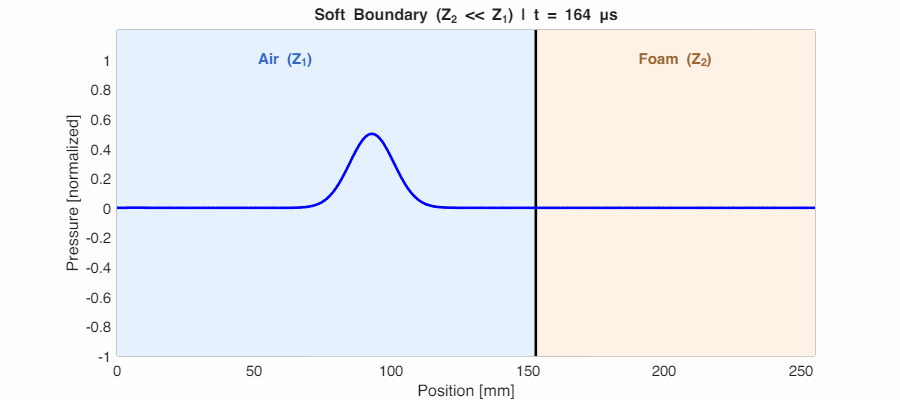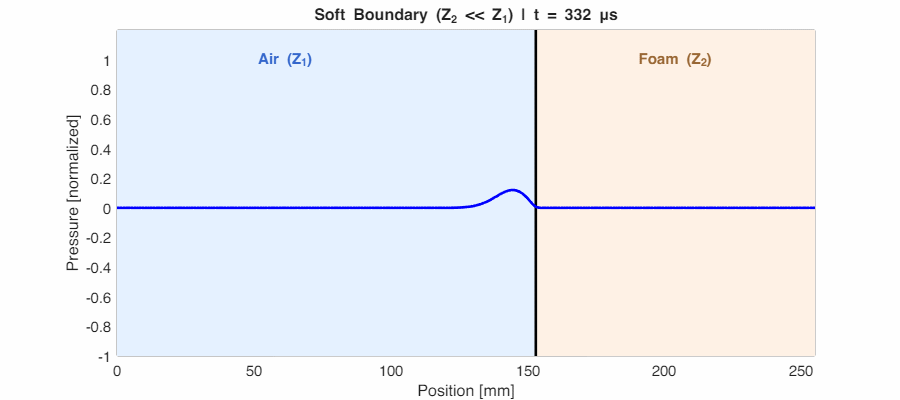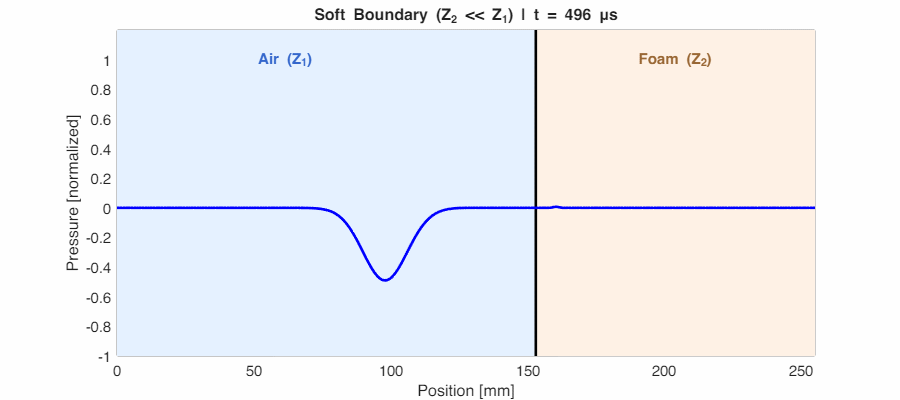
The General Case: Partial Reflection
In reality, most boundaries fall between these extremes. The animation below shows sound traveling from air into water—a moderate impedance mismatch. Part of the wave reflects back, and part transmits forward with reduced amplitude.
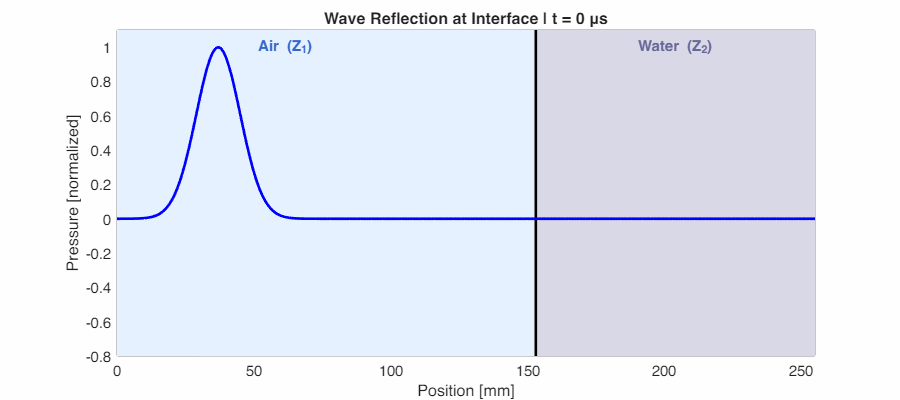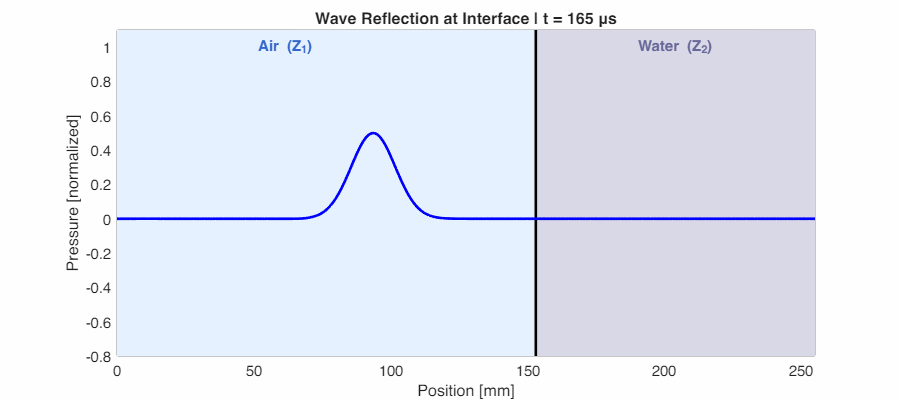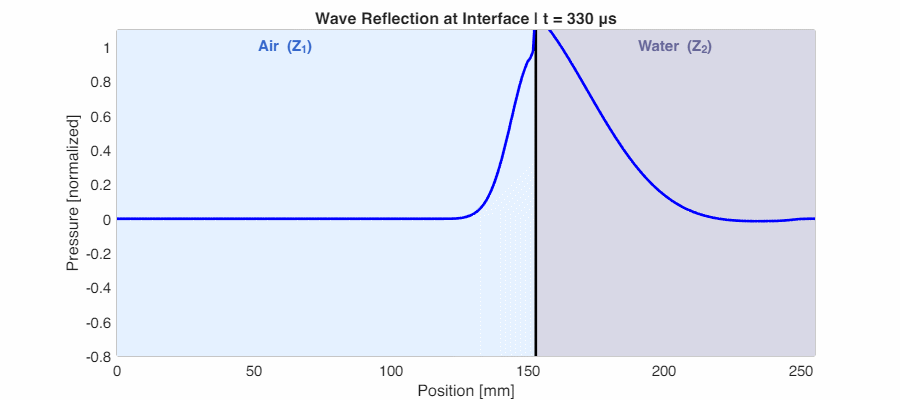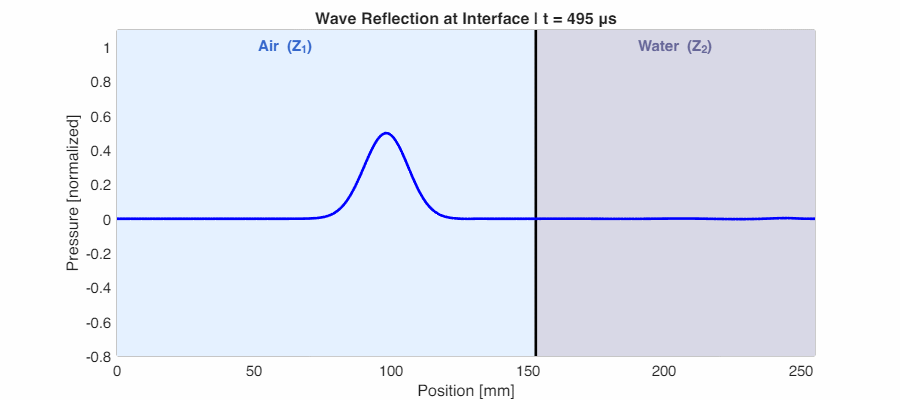
The chart below shows how energy and pressure coefficients vary with impedance ratio. Note that while pressure can exceed 1, energy is always conserved ($R + T = 1$):
Bending the Wave (Snell’s Law)
When sound hits an interface at an angle, it changes direction. This phenomenon—refraction—follows Snell’s Law:
$$ \frac{\sin\theta_1}{\sin\theta_2} = \frac{c_1}{c_2} $$
where $\theta_1$ is the incident angle and $\theta_2$ is the transmitted angle (both measured from the normal).
- If $c_2 > c_1$ (faster medium ahead): the wave bends toward the normal ($\theta_2 < \theta_1$)
- If $c_2 < c_1$ (slower medium ahead): the wave bends away from the normal ($\theta_2 > \theta_1$)
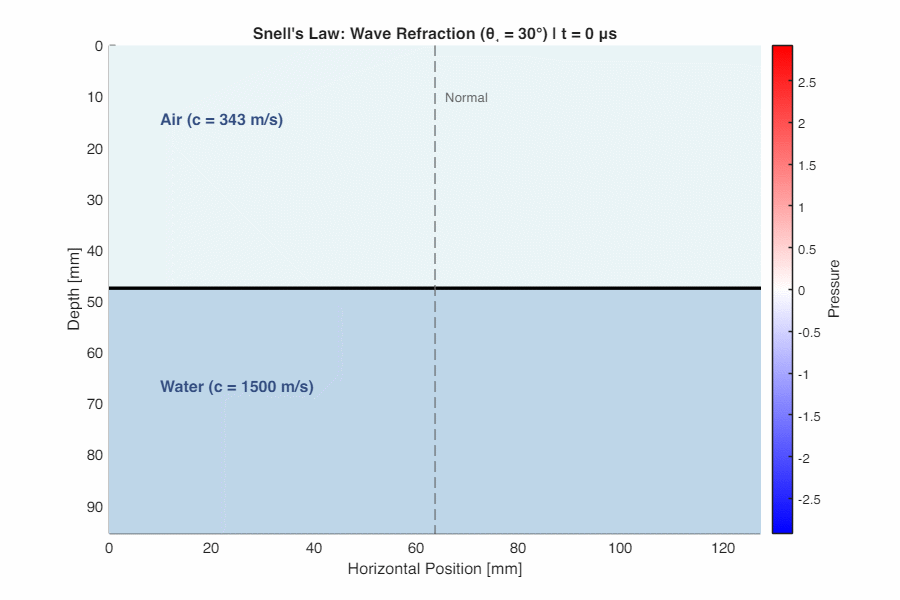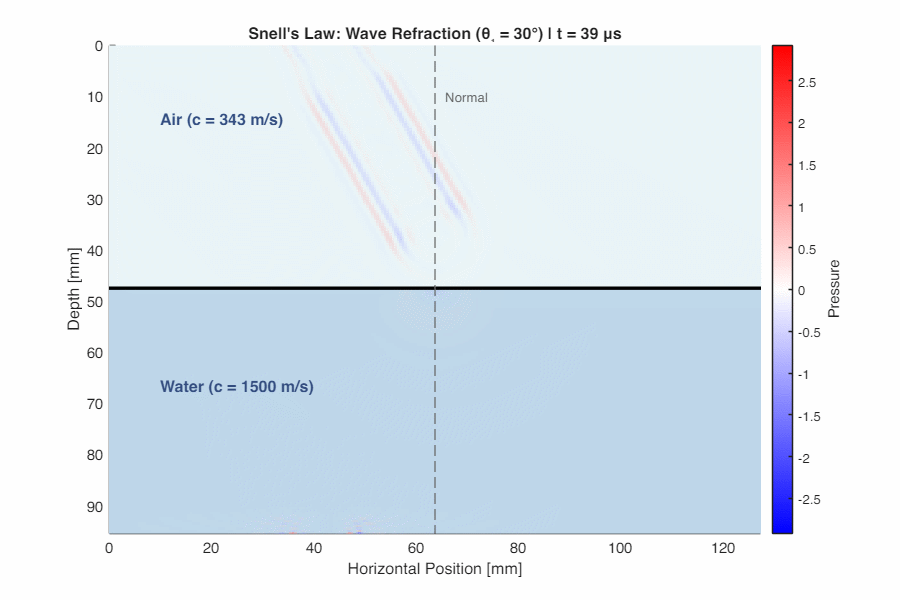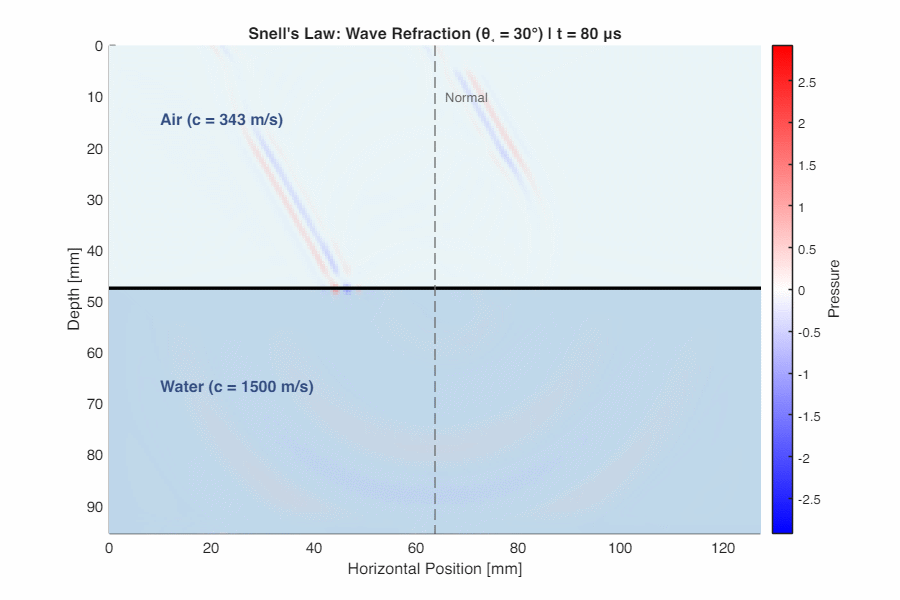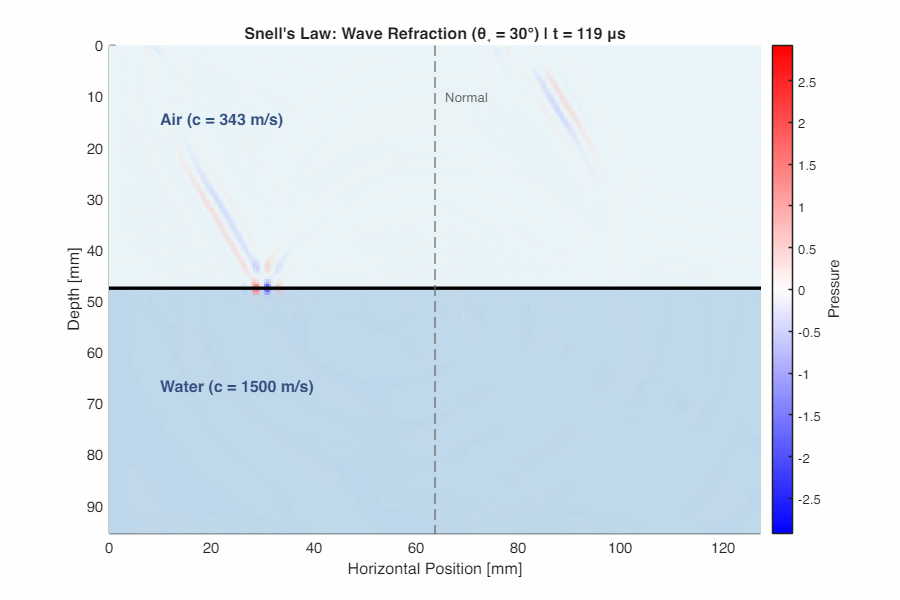
Total Internal Reflection: When sound travels from a faster medium to a slower one ($c_1 > c_2$), there exists a critical angle $\theta_c = \arcsin(c_2/c_1)$ beyond which all sound reflects—none transmits. This explains why sound travels far at night: the atmosphere cools near the ground ($c$ decreases with temperature), creating layers that refract and trap sound near the Earth’s surface.
The Acoustic Highway: Sound in Pipes and Ducts
In engineering, we often force sound to travel down tubes—think of air conditioning ducts or car exhaust pipes. The physics here changes because the wave is “confined.”
The Expansion Muffler
What happens if a pipe suddenly gets wider? You might think the sound just spreads out. Actually, a sudden change in cross-sectional area acts just like a brick wall.
When a pipe’s area changes from $S_1$ to $S_2$, the impedance mismatch causes reflection. Engineers use this to build Expansion Chamber Mufflers. By deliberately forcing exhaust gases through chambers that expand and contract, they force the noise to reflect back toward the engine rather than escaping out the tailpipe.
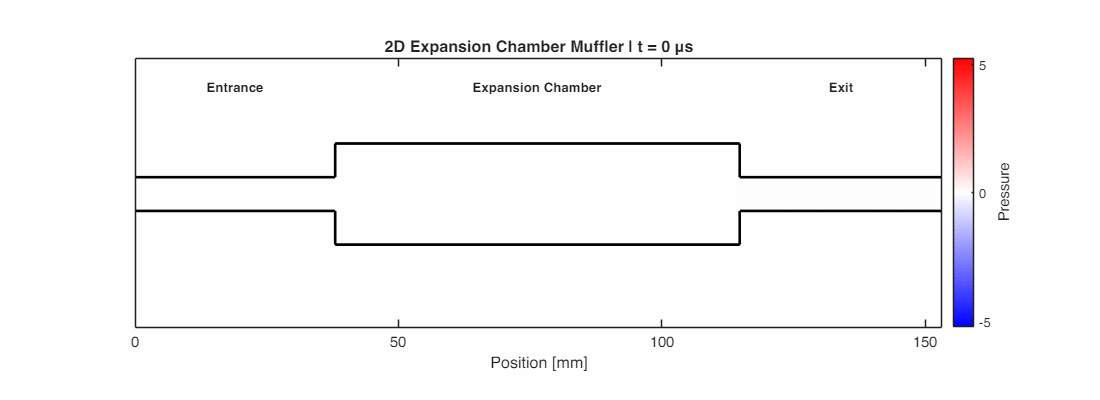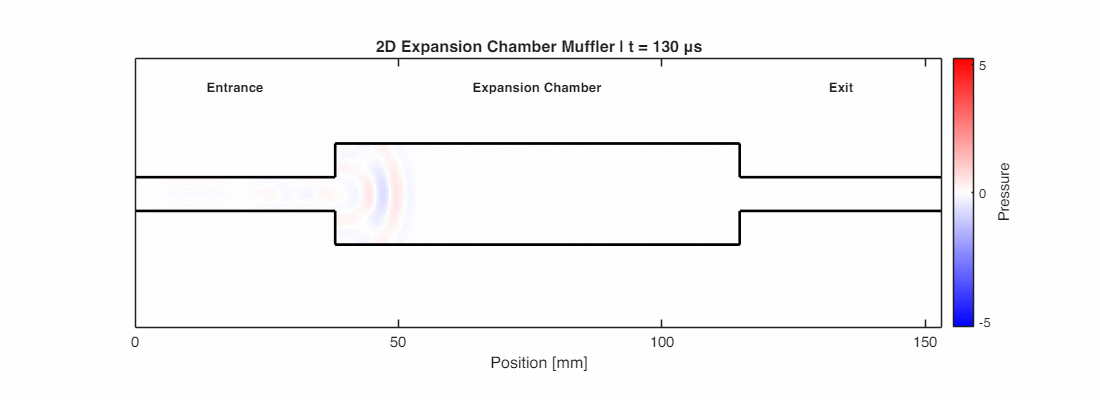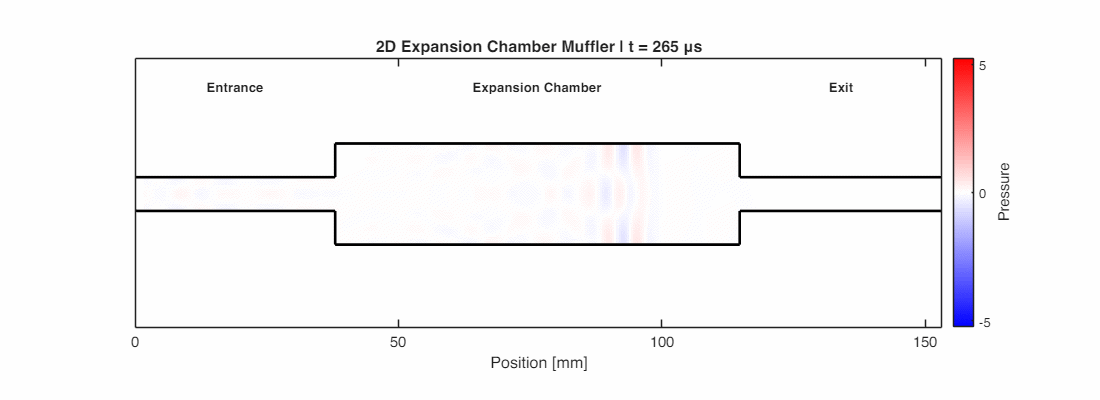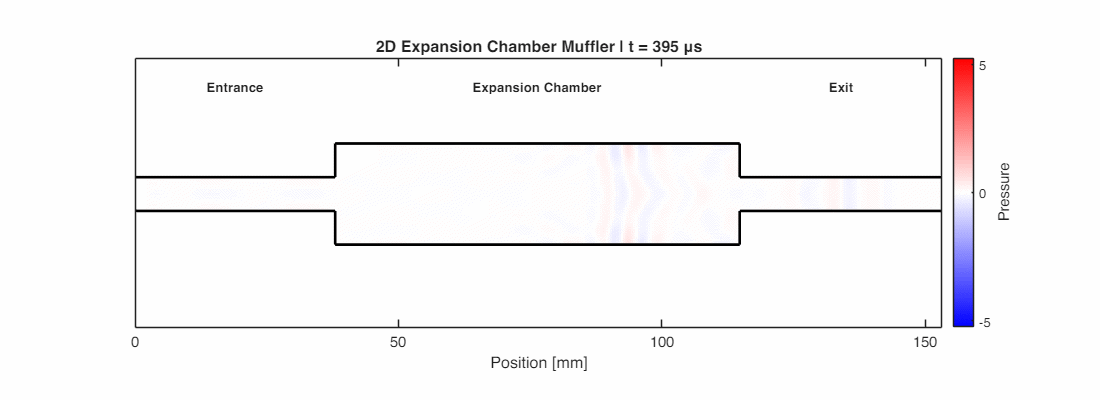
The simulation below shows this in action: when the sound wave hits the sudden expansion (narrow pipe to wide chamber), a strong phase-inverted reflection is generated, sending energy back toward the source.
The Side Branch and Resonators
One of the cleverest tricks in noise control is the Side Branch. If you drill a hole in the side of a main pipe and attach a small resonator (like a bottle), it can kill specific frequencies.
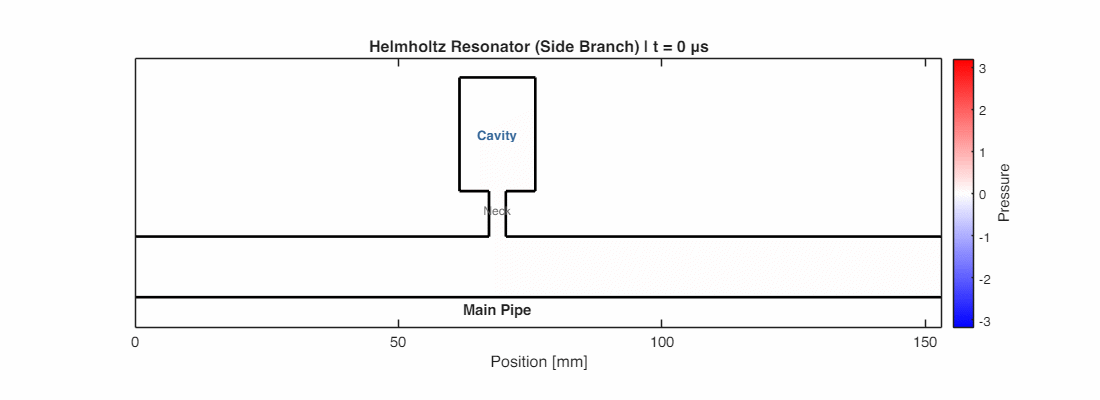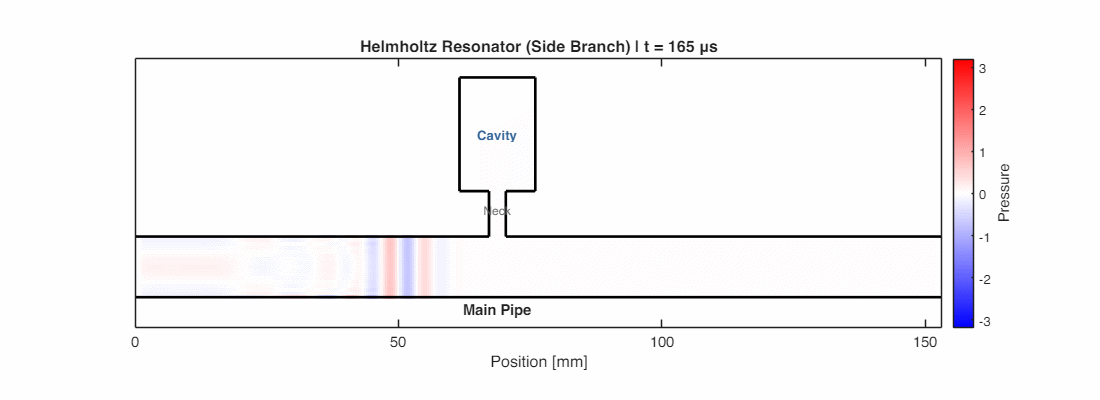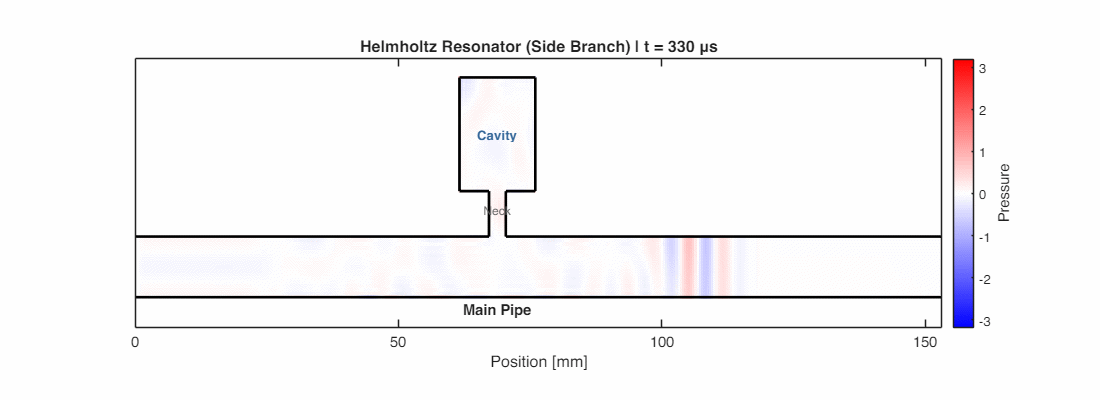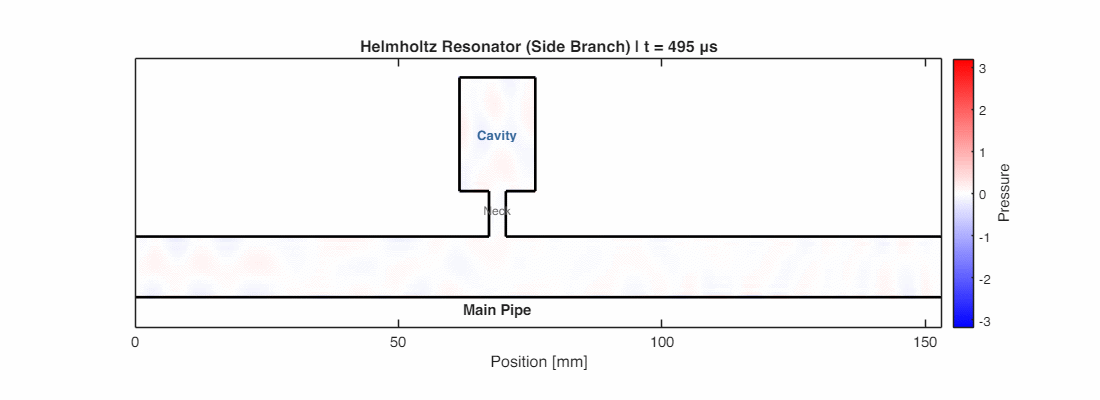
This is the Helmholtz Resonator. At a specific “resonant frequency,” the air in the bottleneck vibrates violently. This creates a massive impedance mismatch at the junction, reflecting the incoming noise back down the main pipe. It acts as a “sound filter,” short-circuiting the noise at that specific pitch.
The resonance frequency is approximately:
$$ f_0 = \frac{c}{2\pi}\sqrt{\frac{S}{V \cdot l_{eff}}} $$
where $S$ is the neck cross-sectional area, $V$ is the cavity volume, and $l_{eff} = l + 0.85d$ is the effective neck length (accounting for “end correction”—the air just outside the neck also participates in the oscillation).
In the simulation below, a wave at the resonant frequency travels down the main pipe. Notice how the air in the neck vibrates intensely, and significantly less energy makes it past the junction—most is reflected back or trapped in the resonator.
Waveguides and Modes
If you shout into a large tunnel, the sound doesn’t just travel straight; it bounces off the walls in complex patterns. These patterns are called Modes.
- Plane Waves vs. Higher Order Modes: At low frequencies, sound travels as a “plane wave”—a flat sheet of pressure moving down the tube. But as the frequency rises, the wavelength gets shorter. Eventually, the wave can fit diagonally across the tube.
- The Cut-off Frequency: There exists a critical threshold called the Cut-off Frequency ($f_c$). Below this frequency, only the simple plane wave can travel. Above it, complex “high-order modes” (waves bouncing in zigzag patterns) begin to propagate.
- For a rectangular duct of width $l_x$, the cut-off happens when the wavelength fits into the duct width: $f_{c} = c_0 / 2l_x$.
- Dispersion: Guided waves exhibit a fascinating property called Dispersion. The “Phase Velocity” (how fast the wave crests move) and the “Group Velocity” (how fast the energy moves) are different. Near the cut-off frequency, the group velocity drops drastically—the energy struggles to move down the tube.
The figure below illustrates the mode shapes—the pressure distribution across the duct height for each mode. The plane wave (Mode 0) has uniform pressure, while higher-order modes exhibit nodes where pressure is zero.
Standing Waves: When Waves Collide
When a wave travels down a tube and hits a hard surface, it reflects. The outgoing wave and the incoming wave crash into each other. At certain frequencies, they lock in place, creating a Standing Wave.
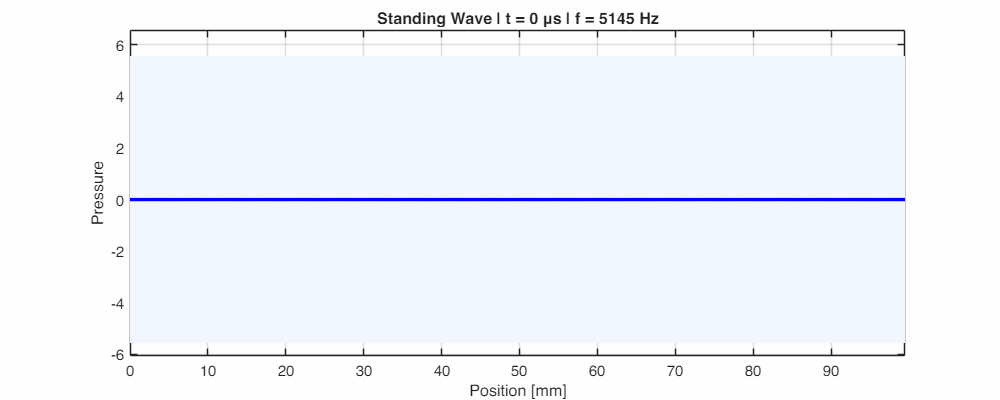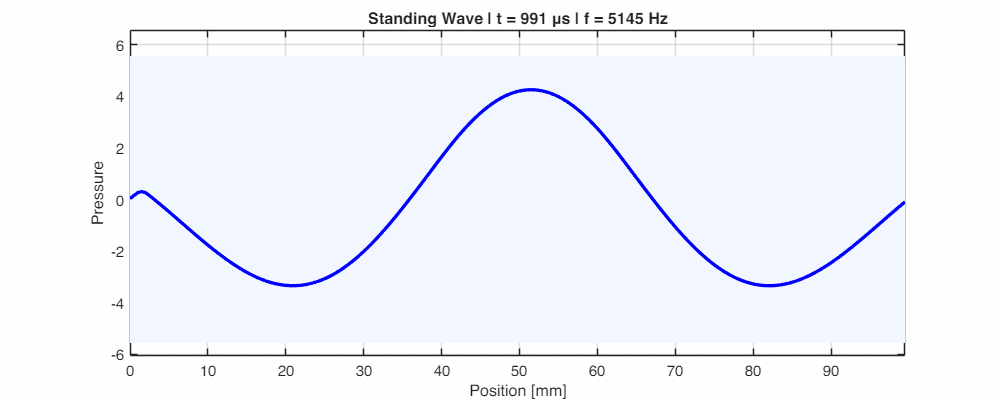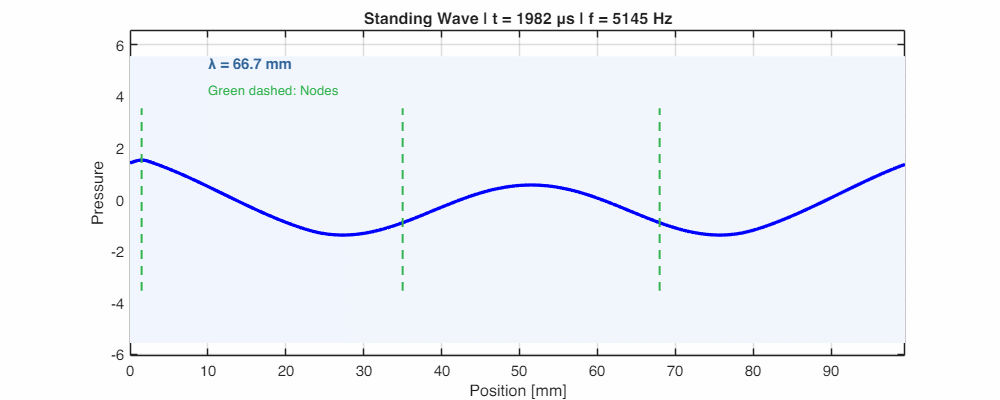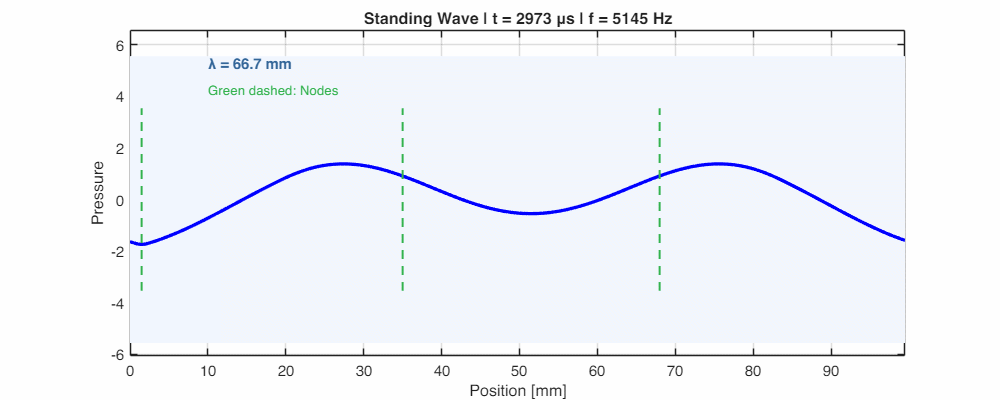
- Nodes and Antinodes: In a standing wave, there are points where the pressure is always zero (Nodes) and points where it is maximum (Antinodes). These are spaced exactly $\lambda/2$ apart.
- Resonance Condition: For a tube of length $L$ closed at one end, resonance occurs when $L = (2n-1)\frac{\lambda}{4}$ (odd quarter-wavelengths). For a tube open at both ends, resonance occurs when $L = n\dfrac{\lambda}{2}$ (half-wavelengths).
- Measuring the Invisible: Acousticians use this phenomenon to measure materials. By using a Standing Wave Tube (Impedance Tube), we can insert a material sample at one end and use a microphone to probe the standing wave pattern.
- The Standing Wave Ratio: If the material is perfectly reflective (hard wall), the standing wave is intense (deep nodes). If the material absorbs sound (like foam), the reflection is weak, and the standing wave “flattens out.” By measuring the ratio of the maximum to minimum pressure, engineers can calculate the exact absorption coefficient of the material.
What’s Next?
We have seen how sound bounces off walls, bends at interfaces, and echoes through pipes. But what happens when we want to stop the sound? How do sponges, foams, and perforated sheets turn acoustic energy into heat?
In the next installment, “Absorption I – Porous Materials,” we will explore the physics of sound absorption—how porous materials, resonant panels, and micro-perforated absorbers trap and dissipate acoustic energy.
References:
- He Lin et al., Theoretical Acoustics and Engineering Applications, Science Press, 2006.
- Ma Dayou, Modern Acoustics Theory Basis, Science Press, 2004.