ML-06: Linear Regression
Learning Objectives
- Understand regression vs classification
- Derive the least squares solution
- Implement linear regression from scratch
- Extend to multiple features
Theory
Regression vs Classification
| Task | Output Type | Example |
|---|---|---|
| Classification | Discrete labels | Spam or not spam |
| Regression | Continuous values | House price prediction |
Classification answers “which category?” while regression answers “how much?”
Linear Model
Where includes the bias term (intercept).
Breaking it down:
- is the intercept (baseline prediction when all features are 0)
- are weights that determine how much each feature contributes
- Each weight tells the model: “for every 1-unit increase in this feature, change the prediction by this amount”
Why Squared Error?
The goal is to find the “best” line through data points. What makes a line optimal? Consider these error metrics:
| Error Metric | Formula | Properties |
|---|---|---|
| Sum of errors | ❌ Positive and negative errors cancel out | |
| Sum of absolute errors | ✓ Works, but not differentiable at 0 | |
| Sum of squared errors | ✓ Differentiable, penalizes large errors more |
Key insight: Squared error is preferred because:
- It’s always positive (no cancellation)
- It’s smooth and differentiable (enables calculus-based optimization)
- It penalizes large errors heavily (one big error is worse than several small ones)
Least Squares Objective
Minimize the sum of squared errors:
In matrix form, where is the design matrix (each row is a sample, each column is a feature):
- = vector of true values
- = vector of predictions
- = squared Euclidean norm
Deriving the Closed-Form Solution
The optimal weights can be derived step by step.
Step 1: Expand the objective function
Expanding the product:
Step 2: Take the gradient with respect to
Using matrix calculus rules:
- (when is symmetric)
Step 3: Set gradient to zero and solve
This is the normal equation — a direct, closed-form solution for linear regression.
Geometric Interpretation
The prediction is the projection of onto the column space of .
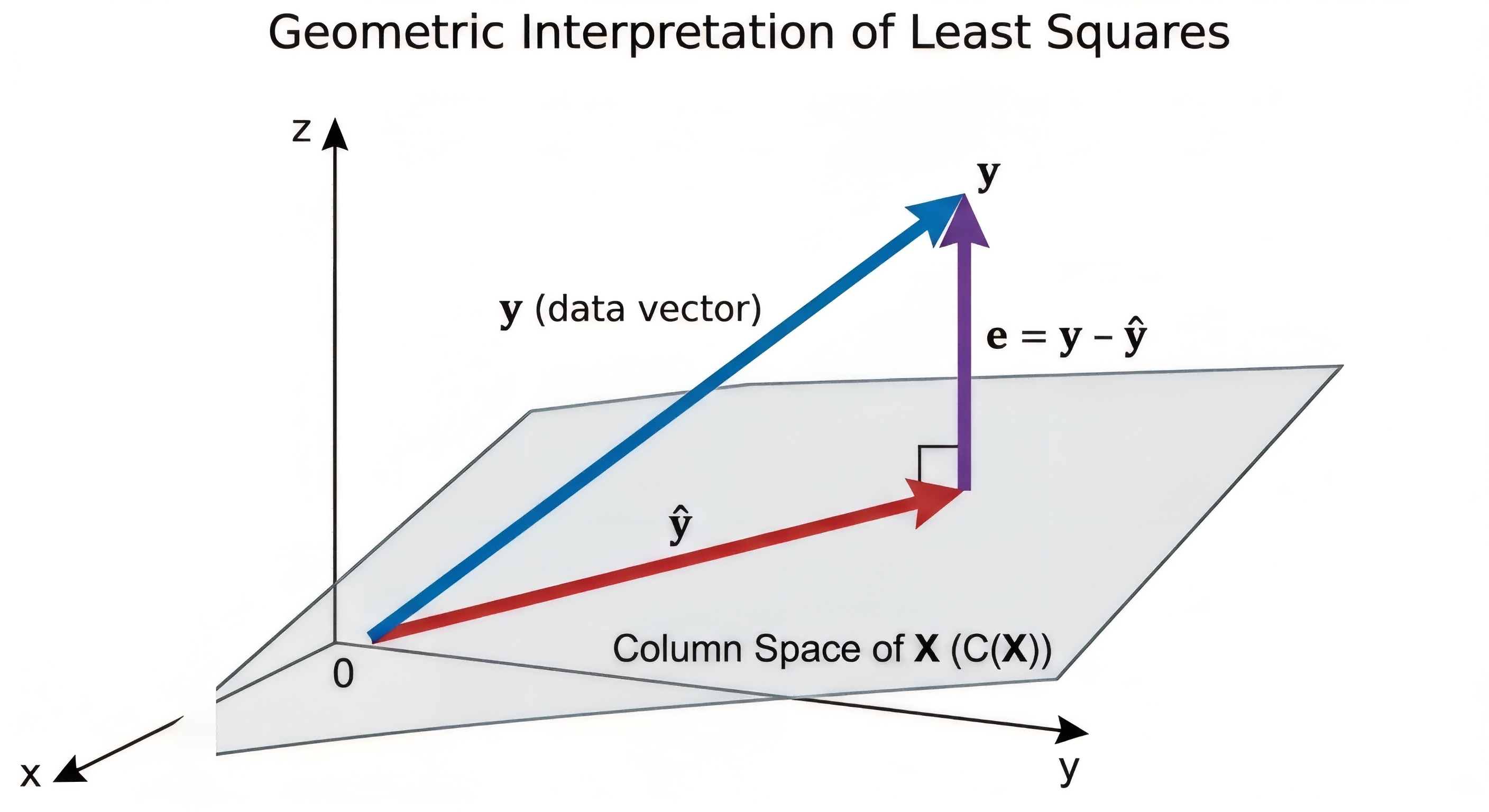
Why projection? The intuition:
- The column space of contains all possible predictions the model can make
- The true might not be in this space (data is rarely perfectly linear)
- The closest point in this space to is its orthogonal projection
- “Closest” in Euclidean distance = minimizing squared error!
The orthogonality condition: The residual vector is perpendicular to every column of :
This is exactly the normal equation rearranged—geometry and calculus yield the same answer.
Understanding R² Score
The coefficient of determination () measures how well the model explains the variance in the data:
Where:
- = Residual sum of squares (unexplained variance)
- = Total sum of squares (total variance)
- = mean of
Interpreting R²:
| R² Value | Interpretation |
|---|---|
| 1.0 | Perfect fit — model explains all variance |
| 0.8 | Good — 80% of variance explained |
| 0.5 | Moderate — half the variance explained |
| 0.0 | Model is no better than predicting the mean |
| < 0 | Model is worse than predicting the mean |
Code Practice
From Scratch Implementation
🐍 Python
| |
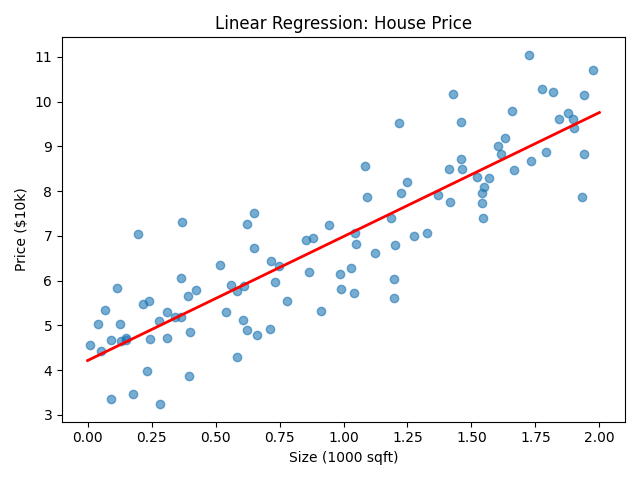
Example: House Price
🐍 Python
| |
Output:
Multiple Linear Regression
🐍 Python
| |
Output:
Deep Dive
Q1: When does the normal equation fail?
The normal equation requires inverting , which can fail or be problematic in several cases:
| Problem | Cause | Solution |
|---|---|---|
| Singular matrix | Features are linearly dependent (e.g., feature_3 = 2 × feature_1) | Remove redundant features or use regularization |
| Near-singular matrix | Features are highly correlated (multicollinearity) | Use Ridge regression (L2 regularization) |
| Large dataset | Matrix inversion is , slow for millions of samples | Use gradient descent (iterative, per step) |
| More features than samples | is not full rank when | Use regularization or dimensionality reduction |
Practical rule of thumb: Use normal equation for small datasets (< 10,000 samples), gradient descent for large ones.
Q2: What does a negative coefficient mean?
A negative weight indicates an inverse relationship: as that feature increases, the prediction decreases (holding other features constant).
Examples:
- House prices: “years since renovation” → negative (older renovation = lower price)
- Test scores: “hours of distraction” → negative (more distraction = lower score)
- Fuel efficiency: “vehicle weight” → negative (heavier = less efficient)
Be careful with interpretation! Coefficients show correlation in the model, not necessarily causation. A negative coefficient for “age” in a house price model might reflect other factors correlated with age.
Q3: Linear regression vs. correlation?
These concepts are related but serve different purposes:
| Aspect | Correlation (r) | Linear Regression |
|---|---|---|
| Purpose | Measure relationship strength | Predict values |
| Output | Single number (-1 to 1) | Prediction function |
| Directionality | Symmetric (r(X,Y) = r(Y,X)) | Asymmetric (X predicts Y) |
| Units | Unitless | Same units as Y |
| Relationship | for simple linear regression | — |
Key insight: The correlation coefficient measures how tightly points cluster around any best-fit line. The relationship shows the proportion of variance explained—both convey the same information in different forms.
Q4: How to handle categorical features?
Linear regression works with numbers, so categorical features must be encoded:
| Method | Example | When to use |
|---|---|---|
| One-hot encoding | Color: [Red, Blue, Green] → [1,0,0], [0,1,0], [0,0,1] | Nominal categories (no order) |
| Ordinal encoding | Size: [S, M, L] → [1, 2, 3] | Ordinal categories (with order) |
Don’t use ordinal encoding for nominal categories! Assigning Red=1, Blue=2, Green=3 implies Blue is “between” Red and Green, which is meaningless.
Summary
| Concept | Formula/Meaning |
|---|---|
| Linear Model | |
| Loss Function | (squared error) |
| Solution | |
| R² Score | Proportion of variance explained |
References
- Bishop, C. “Pattern Recognition and Machine Learning” - Chapter 3
- sklearn Linear Regression Documentation
- Montgomery, D. “Introduction to Linear Regression Analysis”